КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРАПри осевом нагружении стержня в его поперечных сечениях возникают нормальные напряжения сжатия, которые возрастают по мере увеличения нагрузки. Нормальные напряжения, соответствующие критической силе, называются критическими: В последнюю формулу входят две геометрические характеристики площади сечения стержня: минимальный момент инерции Таким образом, Безразмерная величина Определяя значение критической силы, Эйлер исходил из рассмотрения упругой линии изогнутого стержня, поэтому формула Отсюда Стоящая в правой части неравенства постоянная для данного материала безразмерная величина называется предельной гибкостью: Таким образом, применимость формулы Эйлера определяется условием Формула Эйлера применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен.
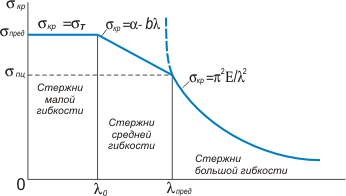
Как правило, многие конструкции имеют стержни с гибкостью меньше предельной. Разработку современных методов расчета на усталость таких стержней начал Ф.С.Ясинский, который предложил приближенные формулы для определения критических напряжений за пределом пропорциональности, проанализировав предварительно обширный экспериментальный материал и построив графические зависимости между и для многих материалов. График зависимости от для стержней из пластичного материала (низкоуглеродистой стали) показан на рисунке 1. В результате исследований подобных графиков стержни условно делятся на три группы. Стержни большой гибкости (
|
, или после подстановки значения критической силы из формулы, 
.
и площадь A. Частное от деления 
представляет собой величину, имеющую единицу площади м2, см2, мм2. Поэтому линейную величину 
называют минимальным радиусом инерции сечения.
и последняя формула принимает вид 
или 
.
называется гибкостью стержня. Она характеризует сопротивляемость стержня потере устойчивости; с увеличением гибкости уменьшается сопротивляемость стержня потере устойчивости. Заметим, что гибкость 
стержня не зависит от материала стержня, а определяется его длиной, формой и размерами сечения.
справедлива только в пределах применимости закона Гука, инача говоря, до тех пор, пока критическое напряжение не превышает предела пропорциональности материала стержня, т. е. при условии 
.
.
.
.
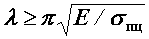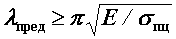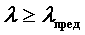), для которых критические напряжения определяются по формуле Ясинского 
, где коэффициенты а и b имеют для каждого материала определенное значение, найденное экспериментально. Некоторые значения этих коэффициентов, а также гибкостей 
и 
, в интервале между которыми применима для данного материала формула Ясинского, приведены в таблице.
), для которых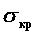 
соответствует 
, т.е. 
для пластичных материалов и 
для хрупких материалов. Такие стержни рассчитывают не на устойчивость, а на прочность, как при простом сжатии.
