Краткие теоретические сведения. В инженерной практике нередко приходится рассматривать равновесие тел, находящихся под действием системы сходящихся сил
В инженерной практике нередко приходится рассматривать равновесие тел, находящихся под действием системы сходящихся сил. С такими задачами, в частности, встречаются при расчетах плоских и пространственных шарнирно-стержневых конструкций – ферм. Совокупность сил, линии действия которых пересекаются в одной точке, называют системой сходящихся сил. Если все силы расположены в одной плоскости, то такую систему называют плоской системой сходящихся сил, а если силы произвольно расположены в пространстве – то пространственной или произвольной системой сходящихся сил. Так как любую силу, действующую на абсолютно твердое тело, можно переносить по ее линии действия в любую точку тела, то, перенося все силы в точку пересечения их линий действия, получаем систему сил, приложенных в одной точке, эквивалентную исходной. Такую систему на основании аксиомы параллелограмма сил можно заменить одной равнодействующей силой, которая приложена в той же точке и равна геометрической сумме этих сил, т.е.
где n – число сил, Из формулы (2.1) следуют условия равновесия тела под действием системы сходящихся сил или условия равновесия системы сходящихся сил:
Последнее выражение записано в векторной форме. Однако для решения задач удобно использовать аналитическую форму условий равновесия, которая требует равенства нулю проекций равнодействующей на координатные оси или сумм проекций на эти оси сил исходной системы:
Здесь x, y, z – оси произвольно выбранной системы координат. Для решения задачи нужно уметь определять проекции сил на оси. В некоторых случаях, особенно в задачах на равновесие произвольной системы сил, удобно пользоваться способом двойного проецирования. Суть способа состоит в том, что вначале находят проекцию силы на плоскость, в которой эта ось расположена, а затем – проекцию полученного вектора на ось. Так, для определения проекций силы
Проекцию силы на ось z находим по обычному правилу, т.е.
|
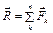, (2.1)
– равнодействующая данной системы сил.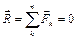
. (2.2)
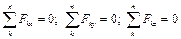. (2.3)
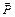на оси 
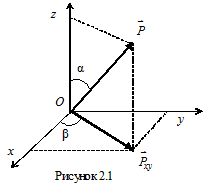(рис. 2.1) вначале находим проекцию силы на плоскость xOy и получаем вектор 
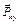, а затем
; 
.
.
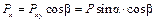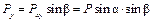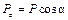