Примеры решения типовых задач. Приведем несколько типичных примеров решения задач
Приведем несколько типичных примеров решения задач. Пример 1. На столб АО (идеальный стержень) высотой 6 м, укрепленный оттяжками АС и AD, которые симметрично расположены относительно плоскости yOz (рис. 2.2), действует сила натяжения провода T = 300 H, которая направлена параллельно оси y. При этом Определить натяжения тросов в оттяжках и усилие, действующее на столб.
Решение 1) В качестве объекта равновесия примем точку А. 2) Активной силой является сила натяжения 3) Отбрасывая связи (оттяжки АD, AC и столб AO), заменим их действие на объект равновесия реакциями 4) Запишем уравнения равновесия (2.3) полученной системы сходящихся сил в принятой системе координат (см. рис. 2.2). Для удобства составим табл. 2.1, которая является вспомогательной, а для сил
Таблица 2.1
Теперь для записи системы уравнений равновесия просуммируем элементы соответствующих строк таблицы и приравняем эти суммы нулю:
T
Здесь Из 1-го уравнения полученной системы следует, что из 2-го уравнения
из 3-го уравнения
Знак «минус» указывает на то, что реакция столба в действительности направлена в сторону, противоположную принятой (см. рис. 2.2). Пример 2. Груз Q весом 100 кН с помощью троса, переброшенного через неподвижный блок Е, прикреплен к точке D и удерживается в равновесии тремя идеальными стержнями, которые шарнирно присоединены к этой точке (рис. 2.3). Определить усилия в стержнях AD, BD и CD, если α = 450, β = 600, γ = 300, ε = 300. Трением в блоке пренебречь.
|

 = 1200, а ОС = ОD = 4, 5 м.
= 1200, а ОС = ОD = 4, 5 м.
 провода АВ.
провода АВ. и
и  .
. и
и  применим способ двойного проецирования.
применим способ двойного проецирования.


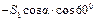




 . Далее находим:
. Далее находим: Н,
Н,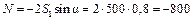 Н.
Н.



