Решение. 1) В качестве объекта равновесия примем всю ферму, которую будем считать абсолютно твердым телом
1) В качестве объекта равновесия примем всю ферму, которую будем считать абсолютно твердым телом. 2) Активными силами, действующими на объект равновесия, будут силы
модули которых
3) Отбрасывая связи (неподвижный цилиндрический шарнир A и подвижный цилиндрический шарнир B), заменим их действие на объект равновесия реакциями 4) Запишем уравнения равновесия (3.1) полученной плоской системы сил в принятой системе координат (см. рис. 3.5). Составим табл. 3.1. Суммируя элементы соответствующих строк таблицы, и приравнивая эти суммы нулю, получим систему уравнений равновесия:
Таблица 3.1
5) Решим полученную систему уравнений, из которых следует: из 1-го
из 3-го
из 2-го
Знаки «минус» у всех реакций указывают на то, что эти реакции в действительности направлены в стороны, противоположные принятым в соответствии с рис. 3.5. По составляющим реакции в шарнире А можно определить модуль и направление реакции
где β – угол, между вектором реакции Для проверки полученного решения составим выражение суммы моментов всех сил, например, относительно точки D
Вычислим относительную погрешность
которая не превышает 1 % и связана с точностью вычислений. Пример 2. Определить реакции жесткой заделки А в ломаном брусе (рис. 3.6.), нагруженном распределенными нагрузками интенсивности которых составляют, соответственно, q1 = 2 кН/м и q2 = 5 кН/м, силой P = 30 кН, и моментом M = 8 кН· м, если a = 2 м, b = 3 м, c = 1 м, d = 2 м, α = 300.
|

 ,
, 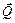 и пары сил с алгебраическими моментами M1, M2. Сила
и пары сил с алгебраическими моментами M1, M2. Сила  кН. Приложена она в середине отрезка длиной a. Силу
кН. Приложена она в середине отрезка длиной a. Силу  и
и  , параллельные координатным осям
, параллельные координатным осям ,
, кН;
кН;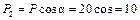 кН.
кН. и
и  . Реакция неподвижного шарнира
. Реакция неподвижного шарнира  и
и  , параллельными координатным осям.
, параллельными координатным осям.





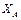









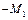
 кН;
кН;
 кН;
кН; кН.
кН. кН,
кН,

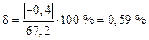 ,
,



