Краткие теоретические сведения. Задачи на равновесие тела, находящегося под действием произвольной пространственной системы сил, представляют собой наиболее общий случай задач о равновесии
Задачи на равновесие тела, находящегося под действием произвольной пространственной системы сил, представляют собой наиболее общий случай задач о равновесии абсолютно твердого тела и имеют важное значение в технике. Новыми элементами при составлении уравнений равновесия является вычисление моментов сил и моментов пар сил относительно координатных осей. При решении данного типа задач необходимо пользоваться понятием вектора-момента пары сил в отличие от алгебраического момента пары. Моментом силы относительно некоторой оси называют скалярную величину, равную проекции на эту ось вектора-момента силы относительно любой точки на этой оси. Из приведенного определения следует другое правило вычисления указанной величины, часто используемое при непосредственном решении задач. Его формулируют следующим образом: «Момент силы относительно оси равен взятому с соответствующим знаком произведению модуля проекции силы на плоскость, перпендикулярную данной оси, на ее плечо относительно точки пересечения оси с плоскостью». Знак «плюс» ставят тогда, когда поворот тела вокруг данной оси с ее положительного направления наблюдается происходящим против хода стрелки часов, и знак «минус» – в противном случае. Другими словами, момент силы относительно оси равен алгебраическому моменту проекции силы на плоскость, перпендикулярную данной оси, относительно точки пересечения этой плоскости с осью. Из сказанного вытекает, что момент силы относительно оси равен нулю в случаях, если сила параллельна оси (тогда проекция силы на плоскость, перпендикулярную данной оси, равна нулю) или если линия действия силы пересекает ось (тогда плечо равно нулю). Оба указанных случая можно объединить в один – момент силы относительно оси равен нулю, если сила и ось расположены в одной плоскости. Когда, например, оси x, y, z являются тремя взаимно перпендикулярными осями, проведенными из любой точки тела, и нужно определить момент силы
где 1) определить проекцию силы на плоскость, перпендикулярную данной оси – вектор 2) найти точку пересечения данной плоскости с осью (в рассматриваемом примере это точка О);
Если сила
Действие пары сил на твердое тело полностью определяется вектором-моментом пары. В теории пар сил доказано, что вектор-момент пары сил – это свободный вектор, не имеющий точки приложения, другими словами, такой вектор может считаться приложенным в любой точке тела. Напомним, что вектор-момент пары сил – это вектор, перпендикулярный плоскости, в которой расположены силы пары, а его модуль равен произведению модуля одной из сил пары на плечо пары. Направлен вектор-момент пары сил так, что вращение тела силами пары наблюдается с его конца происходящим против хода стрелки часов. Две пары сил эквивалентны, если равны их векторы-моменты. Две и более пар сил, действующих на абсолютно твердое тело, можно заменить одной парой, векторный момент которой равен геометрической сумме векторов-моментов этих пар. Если на твердое тело действуют пары сил, то их моменты относительно некоторой оси равны проекциям на данную ось векторов-моментов этих пар. Для произвольной пространственной системы сил необходимыми и достаточными условиями равновесия является равенство нулю главного вектора и главного момента этой системы сил относительно произвольной точки:
Аналитические условия равновесия для произвольно выбранной системы декартовых координат имеют вид:
(4.4)
|

 относительно оси z (рис. 4.1), то можно воспользоваться формулой
относительно оси z (рис. 4.1), то можно воспользоваться формулой (4.1)
(4.1)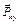 – векторная величина, равная проекции силы на плоскость, перпендикулярную оси z, т.е. на плоскость xOy; h – плечо силы
– векторная величина, равная проекции силы на плоскость, перпендикулярную оси z, т.е. на плоскость xOy; h – плечо силы  в) вычислить алгебраический момент силы
в) вычислить алгебраический момент силы  (4.2)
(4.2) (4.3)
(4.3)




