Решение. 1) Объектом равновесия является вся конструкция (вал с прикрепленными к нему стержнями)
1) Объектом равновесия является вся конструкция (вал с прикрепленными к нему стержнями). 2) Активными силами, действующими на объект равновесия, будут силы 3) Отбрасывая связи (подпятник A и неподвижный цилиндрический шарнир B), заменим их действие на объект равновесия реакциями 4) Запишем уравнения равновесия (4.4) полученной пространственной системы сил в принятой системе координат (см. рис. 4.2) с помощью табл. 4.1. Таблица 4.1
Продолжение табл. 4.1
Рассмотрим более подробно определение момента силы относительно оси на примере силы Способ 1. Определим проекции силы – на плоскость, перпендикулярную оси x, – на плоскость, перпендикулярную оси y, – на плоскость, перпендикулярную оси z, При определении моментов силы
При определении моментов силы
Способ 2. Запишем проекции силы
и координаты точки приложения силы
Используя аналитические выражения (4.2), получим
Cуммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:
5) Решим полученную систему, начиная с уравнений, содержащих не более одной неизвестной силы. Так, из последнего уравнения определим
Затем с учетом найденного значения Q решим 5-е уравнение и определим
Далее из уравнений находим: из 1-го
из 3-го
из 4-го
и, наконец, из 2-го
Пример 2. Определить реакции жесткой пространственной заделки А для невесомой рамы ABC (рис. 4.3.), расположенной в горизонтальной плоскости xOy и нагруженной силой
|

 ,
, 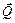 и пара сил, вектор-момент которой
и пара сил, вектор-момент которой  .
. и
и  . Реакция подпятника представлена составляющими
. Реакция подпятника представлена составляющими  ,
,  и
и  , а неподвижного цилиндрического шарнира – составляющими
, а неподвижного цилиндрического шарнира – составляющими 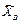 и
и  , параллельными соответствующим координатным осям.
, параллельными соответствующим координатным осям.

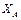

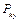










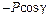









 :
:



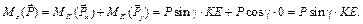
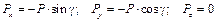
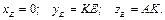

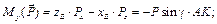









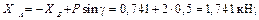


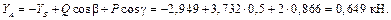
 силами
силами  и
и  , образующими пару сил, вектор-момент которой
, образующими пару сил, вектор-момент которой  . Кроме того, с помощью троса, переброшенного через неподвижный блок D и прикрепленного к концу С рамы, удерживается в равновесии груз весом
. Кроме того, с помощью троса, переброшенного через неподвижный блок D и прикрепленного к концу С рамы, удерживается в равновесии груз весом  = 2 кН. Сила
= 2 кН. Сила 



