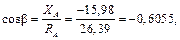Решение. 1) В качестве объекта равновесия примем брус AB
1) В качестве объекта равновесия примем брус AB. 2) Активными силами, действующими на объект равновесия, будут
Модули этих составляющих:
3) Отбрасывая связь (плоскую жесткую заделку A), заменим ее действие на объект равновесия реакцией 4) Запишем уравнения равновесия (3.1) полученной плоской системы сил в принятой системе координат (см. рис. 3.6), составив предварительно табл. 3.2. Таблица 3.2
Суммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:
5) Решим полученную систему уравнений и найдем: из 1-го
из 2-го
из 3-го
Знак «минус» у реакции XA указывает на то, что эта реакция в действительности направлена в сторону, противоположную ранее принятой (см. рис. 3.6.). По составляющим реакции в шарнире А можно определить ее модуль и направление
где β – угол, между вектором реакции Для проверки полученного решения составим выражение суммы моментов всех сил, например, относительно точки В:
В данном примере относительная погрешность оказалась равной нулю. Пример 3. Определить реакцию шарнира A и усилие в идеальном стержне BC балки (рис. 3.7.), нагруженной равномерной распределенной нагрузкой интенсивностью q = 4 кН/м и удерживающей груз весом P = 6 кН с помощью троса. Он переброшен через неподвижный блок В. Трение в блоке отсутствует. Размеры на рисунке даны в метрах. Точки A, B и D считать расположенными на одной прямой.
|

 ,
,  ,
,  и пара сил, алгебраический момент которой M. Силы
и пара сил, алгебраический момент которой M. Силы 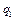 и
и  . Их модули:
. Их модули:  кН;
кН;  кН. Приложены они в середине отрезков длиной b и d (см. рис. 3.6.). Силу
кН. Приложены они в середине отрезков длиной b и d (см. рис. 3.6.). Силу  и
и  , параллельные координатным осям,
, параллельные координатным осям, .
. кН;
кН;  .
. , которая представлена составляющими
, которая представлена составляющими  и
и  , параллельными координатным осям, и парой сил с алгебраическим моментом MА.
, параллельными координатным осям, и парой сил с алгебраическим моментом MА.


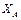




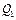







 кН;
кН;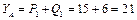 кН;
кН;
 кН· м.
кН· м.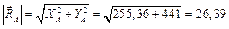 кН,
кН,