Решение. 1) В качестве объекта равновесия примем балку AD
1) В качестве объекта равновесия примем балку AD. 2) Активными силами, действующими на объект равновесия, будут сила 3) Отбрасывая связи (неподвижный цилиндрический шарнир A и идеальный стержень BC), заменим их действие на объект равновесия реакцией 4) Запишем уравнения равновесия (3.2) полученной плоской системы сил в принятой системе координат (см. рис. 3.7), составив предварительно табл. 3.3.
Таблица 3.3
Cуммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:
5) Решим полученную систему уравнений и найдем: из 2-го
из 1-го
из 3-го
Знак «минус» у реакции XA указывает на то, что эта реакция в действительности направлена в сторону, противоположную ранее принятой (см. рис. 3.7). Для проверки полученного решения составим выражение суммы проекций всех сил на ось y:
В данном примере относительная погрешность также оказалась равной нулю.
Вопросы для самоконтроля 1. Какую совокупность сил называют произвольной плоской системой сил? 2. Как определяют алгебраический момент силы относительно точки? 3. Что называют плечом силы относительно точки? 4. Как принято устанавливать знак алгебраического момента силы относительно точки? 5. Когда удобно использовать теорему Вариньона для нахождения момента силы относительно точки? 6. Какую систему сил называют парой сил и как определяют алгебраический момент пары сил? 7. Какими основными свойствами обладает пара сил? 8. Какую эквивалентную замену применяют для равномерно распределенной нагрузки? 9. Как записывают условия равновесия произвольной плоской системы сил в основной и в дополнительных формах? 10. Выполнение каких условий необходимо для разрешимости уравнений равновесия? 11. Каким образом можно проверить правильность решения задачи и оценить его точность?
|

 , направленная вдоль нити в месте крепления, и сила
, направленная вдоль нити в месте крепления, и сила 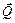 , которая является равнодействующей распределенной нагрузки q и модуль которой
, которая является равнодействующей распределенной нагрузки q и модуль которой  кН.
кН. . Она представлена составляющими
. Она представлена составляющими  и
и  , параллельными координатным осям, и усилием в стержне
, параллельными координатным осям, и усилием в стержне  , которое направлено по прямой, соединяющей шарниры B и C.
, которое направлено по прямой, соединяющей шарниры B и C.
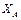





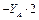





 кН;
кН;
 кН;
кН; кН.
кН.




