Центр параллельных сил. Центр тяжести
В статике доказывают, что если система параллельных сил имеет равнодействующую, то существует точка, притом только одна, через которую проходит ее линия действия. Эту точку называют центром параллельных сил. Центр параллельных сил обладает одним важным свойством – если все силы повернуть относительно параллельных осей, проходящих через точки их приложения на один и тот же угол, то равнодействующая системы этих сил повернется на тот же угол относительно аналогичной оси, проходящей через центр параллельных сил. Рассмотрим тело произвольной формы, находящееся в поле сил тяжести Земли. При этом на каждый элементарный объем рассматриваемого тела действует сила тяжести
где
Когда тело однородно, Силы тяжести, действующие на каждый элементарный объем тела, направлены к центру Земли. Если размерами тела по отношению к размерам Земли пренебречь, то систему сил тяжести можно считать системой параллельных сил, направленных в одну сторону. Такая система всегда имеет равнодействующую, а, следовательно, и центр параллельных сил. Центр системы сил тяжести, действующих на тело со стороны Земли, называют центром тяжести тела. Если тело рассматривается в системе отсчета с центром в точке О и с координатными осями x, y, z (рис. 1.8), то радиус-вектор центра тяжести и его координаты определяют по формуле:
Здесь Центр тяжести не изменяет своего положения по отношению к телу при любой его ориентации относительно Земли. Центр тяжести – геометрическая точка, которая может не принадлежать телу, но обязательно с ним жестко связана. Если тело однородно, т.е.
Формулы, по которым определяют координаты центров тяжести однородных тел, имеют следующий вид: – центр тяжести объема
– центр тяжести поверхности
– центр тяжести линии
где соответственно величины: V – объема тел; S – площади поверхности тела; L – длины тела, по которым берут интегралы. Для нахождения центров тяжести тел используют непосредственно приведенные формулы, а также правила симметрии и методы разбиения сложных тел на более простые, для которых легче определить положения их центров тяжести. В отдельных случаях положения центров тяжести тел находят экспериментальным путем.
|

 , (1.3)
, (1.3) – удельный вес элемента объема
– удельный вес элемента объема  ,
, .
. не зависит от координат.
не зависит от координат.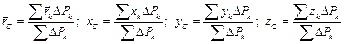 . (1.4)
. (1.4) – модуль силы тяжести, действующей на элементарный объем
– модуль силы тяжести, действующей на элементарный объем  , где
, где  , то вместо понятия центр тяжести можно использовать центр тяжести объема, занимаемого телом. Аналогично, если однородное тело представляет собой тонкую пластинку или оболочку постоянной толщины, либо тонкий криволинейный стержень постоянной толщины, то центр тяжести такого тела называют центром тяжести поверхности или линии.
, то вместо понятия центр тяжести можно использовать центр тяжести объема, занимаемого телом. Аналогично, если однородное тело представляет собой тонкую пластинку или оболочку постоянной толщины, либо тонкий криволинейный стержень постоянной толщины, то центр тяжести такого тела называют центром тяжести поверхности или линии.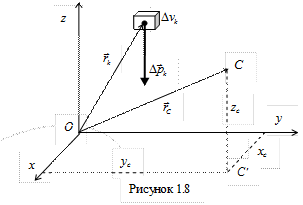
 ; (1.5)
; (1.5)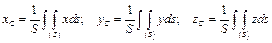 ; (1.6)
; (1.6) , (1.7)
, (1.7)


