Жесткая пластина  (рис. 1.2) имеет в точке
(рис. 1.2) имеет в точке  неподвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. Определить реакции в точках
неподвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. Определить реакции в точках  и
и 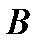 , вызываемые действующими нагрузками, если
, вызываемые действующими нагрузками, если  ,
,  ,
, 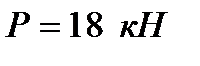 ,
, 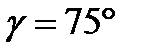 ,
,  ,
,  ,
,  .
.
Решение. 1. Рассмотрим равновесие пластины. Проведем координатные оси  и изобразим действующие на пластину силы: силу
и изобразим действующие на пластину силы: силу 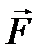 , пару сил с моментом
, пару сил с моментом 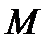 , натяжение троса
, натяжение троса  (по модулю
(по модулю  ) и реакции связей
) и реакции связей  ,
, 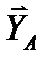 ,
,  (реакцию неподвижной шарнирной опоры
(реакцию неподвижной шарнирной опоры  изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
Таблица 1.1
| Цифры шифра
| 1 цифра шифра
| 2 цифра шифра
| 3 цифра шифра
|
| Схема
|
|
|
|
|

| 
| 
| 
|
| Точка приложе-ния
| 
| Точка приложе-ния
| 
| Точка приложе-ния
| 
| Точка приложе-ния
|

|
|
|
| H
|
| -
| -
| -
| -
| K
|
|
|
|
| -
| -
| D
|
| E
|
| -
| -
|
|
|
| K
|
| -
| -
| -
| -
| E
|
|
|
|
| -
| -
| K
|
| H
|
| -
| -
|
|
|
| D
|
| -
| -
| -
| -
| E
|
|
|
|
| -
| -
| H
|
| -
| -
| D
|
|
|
|
| E
|
| -
| -
| K
|
| -
| -
|
|
|
| -
| -
| D
|
| -
| -
| H
|
|
|
|
| H
|
| -
| -
| D
|
| -
| -
|
|
|
| -
| -
| E
|
| K
|
| -
| -
|
| Схема 1
| Схема 2
| Схема 3
|
|
|
|
|
| Схема 4
| Схема 5
| Схема 6
|
|
|
|
|
| Схема 7
| Схема8
| Схема9
|
|
|
|
|
| Схема 10
|
|
|
Рис. 1.1 Схемы к задаче 1.1
Рис. 1.2. Пример решения задачи 1.1.
2. Для получения плоской системы сил составим три уравнения равновесия. При вычислении момента силы  относительно точки
относительно точки  воспользуемся теоремой Вариньона, т.е. разложим силу
воспользуемся теоремой Вариньона, т.е. разложим силу  на составляющие
на составляющие  и
и  (
(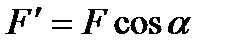 ,
,  ) и учтем, что
) и учтем, что  .
.
Получим:
 ,
,  ;
;
 ,
,  ;
;
 ,
,
 .
.
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Ответ:  ,
,  ,
,  . Знаки указывают, что силы
. Знаки указывают, что силы  и
и 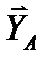 имеют направления, противоположенные показанным на рис. 1.2.
имеют направления, противоположенные показанным на рис. 1.2.

 (рис. 1.2) имеет в точке
(рис. 1.2) имеет в точке  неподвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. Определить реакции в точках
неподвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. Определить реакции в точках 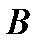 , вызываемые действующими нагрузками, если
, вызываемые действующими нагрузками, если  ,
,  ,
, 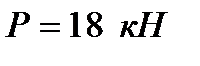 ,
, 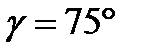 ,
,  ,
,  ,
,  .
. и изобразим действующие на пластину силы: силу
и изобразим действующие на пластину силы: силу 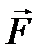 , пару сил с моментом
, пару сил с моментом 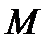 , натяжение троса
, натяжение троса  (по модулю
(по модулю  ) и реакции связей
) и реакции связей  ,
, 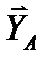 ,
,  (реакцию неподвижной шарнирной опоры
(реакцию неподвижной шарнирной опоры 







 относительно точки
относительно точки  на составляющие
на составляющие  и
и  (
(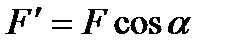 ,
,  ) и учтем, что
) и учтем, что  .
. ,
,  ;
; ,
,  ;
; ,
, .
. ,
,  ,
,  . Знаки указывают, что силы
. Знаки указывают, что силы 


