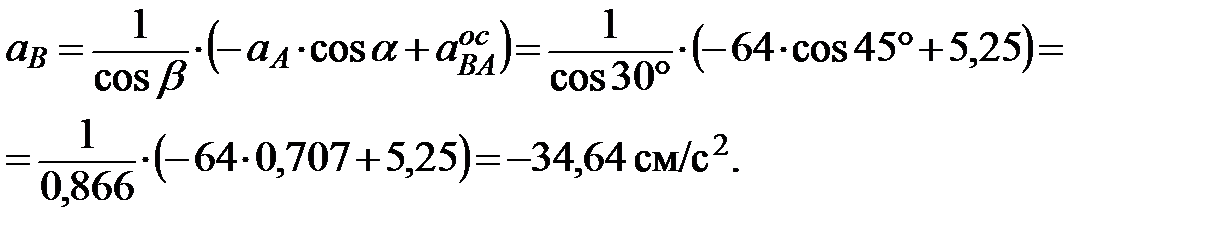Пример решения задачи 2.3
Условие. Кривошип ОА длиной R=64 см вращается вокруг неподвижной оси О с постоянной угловой скоростью w=1 рад/с и приводит в движение шатун АВ длиной L=72 см и ползун В. Для положения механизма, заданного значениями углов a=45°, b=30, ° найти скорость и ускорение ползуна В. Схема механизма приведена на рис. 2.8.
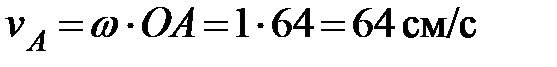 . Для определения скорости точки В найдем положение мгновенного центра скоростейР, для чего покажем направление скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их скоростям vA и vB. Точка пересечения перпендикуляров будет являться мгновенным центром скоростей Р (см. рис. 2.8). . Для определения скорости точки В найдем положение мгновенного центра скоростейР, для чего покажем направление скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их скоростям vA и vB. Точка пересечения перпендикуляров будет являться мгновенным центром скоростей Р (см. рис. 2.8).
Рассмотрим движение шатуна в данный момент времени как вращательное относительно оси, проходящей через мгновенный центр скоростей Р перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна в этом случае определяется из соотношения Расстояния АР и BP определим из решения треугольника АВР, применив теорему синусов. Для заданного положения механизма получим
Подставив найденные значения расстояний в соответствующие формулы, получим 2. Для определения ускорения ползуна B воспользуемся векторным равенством:
где
Ускорение точки А кривошипа при равномерном вращении вокруг неподвижной оси О состоит только из осестремительной составляющей, модуль которой определяется формулой Осестремительное ускорение точки В при ее вращении вокруг полюса А:
 обычным способом не представляется возможным, так как величина углового ускорения звена АВ неизвестна. Несмотря на это обстоятельство, векторное равенство (1) позволяет найти ускорение ползуна В. Для этого воспользуемся тем, что нам известно направления вектора обычным способом не представляется возможным, так как величина углового ускорения звена АВ неизвестна. Несмотря на это обстоятельство, векторное равенство (1) позволяет найти ускорение ползуна В. Для этого воспользуемся тем, что нам известно направления вектора  (он перпендикулярен ускорению (он перпендикулярен ускорению  ) и вектора ускорения искомого ускорения ) и вектора ускорения искомого ускорения  (вдоль прямолинейной траектории точки В). (вдоль прямолинейной траектории точки В).
Проведем вектор ускорения
Знак минус показывает, что истинное направление ускорения точки В противоположно принятому. 3. КОНТРОЛЬНАЯ РАБОТА ПО РАЗДЕЛУ «ДИНАМИКА»
|


 , а скорость ползуна В как вращательная – из соотношения
, а скорость ползуна В как вращательная – из соотношения 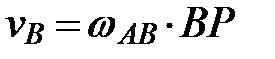 .
. , откуда
, откуда

 . Направления скоростей показаны на рис. 2.8.
. Направления скоростей показаны на рис. 2.8.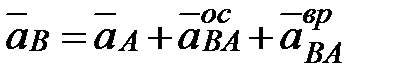 , (1)
, (1) – ускорение точки А, выбранной за полюс;
– ускорение точки А, выбранной за полюс; . Вектор ускорения точки А направлен к оси вращения (рис.2.9),
. Вектор ускорения точки А направлен к оси вращения (рис.2.9), 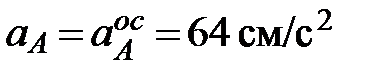 .
. .
.
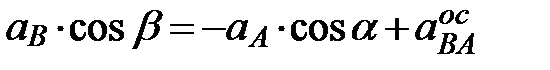 . Отсюда
. Отсюда