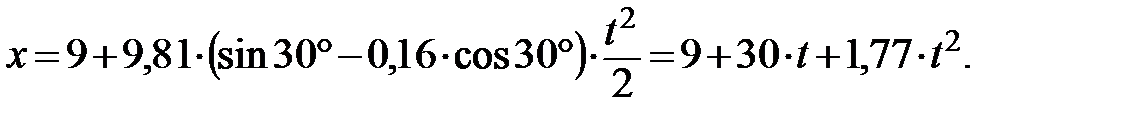Пример решения задачи 3.1
Условие. Груз весом Р движется вниз по шероховатой наклонной плоскости, составляющей угол a=30°с горизонтом. Коэффициент трения скольжения груза о плоскость f=0, 16. В начальный момент груз находился в положении Мо на расстоянии a=9 м от начала координат и имел скорость v0=30 м/с. Определить уравнение движения груза в заданной системе координат (рис. 3.2).
  Решение. 1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (шероховатой наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения Fтр. Тогда тело будет двигаться под действием системы трех сил (Р, N, Fтр). Решение. 1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (шероховатой наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения Fтр. Тогда тело будет двигаться под действием системы трех сил (Р, N, Fтр).
1. Примем тело за материальную точку. Проектируя основное уравнение динамики точки на оси декартовых координат Оx и Оy (ось Оx совпадает с направлением движения точки), получим два дифференциальных уравнения:
Так как тело движется прямолинейно вдоль оси Оx, то проекция ускорения на ось Оy равна нулю, следовательно, уравнение (3.2) примет вид Сила трения по закону Кулона равна
После замены
Для понижения порядка уравнения произведем замену
Разделив переменные, проинтегрируем дифференциальное уравнение с учетом начальных условий (при t=0, vx=v0):
|


 Здесь m – масса точки;
Здесь m – масса точки;  – проекции ускорения точки на соответствующие оси.
– проекции ускорения точки на соответствующие оси. .
. . С учетом этого выражения дифференциальное уравнение (3.1) примет следующий вид:
. С учетом этого выражения дифференциальное уравнение (3.1) примет следующий вид: .
. , где
, где  – ускорение свободного падения тела, и очевидных преобразований получим следующее дифференциальное уравнение второго порядка:
– ускорение свободного падения тела, и очевидных преобразований получим следующее дифференциальное уравнение второго порядка: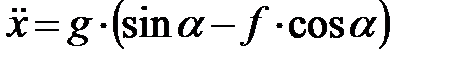 .
. , получим дифференциальное уравнение первого порядка с разделяющимися переменными:
, получим дифференциальное уравнение первого порядка с разделяющимися переменными: .
. Произведем замену для понижения порядка уравнения
Произведем замену для понижения порядка уравнения 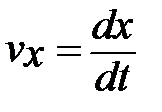 и, разделив переменные, проинтегрируем дифференциальное уравнение второй раз с учетом начальных условий (при t=0 x=x0=a):
и, разделив переменные, проинтегрируем дифференциальное уравнение второй раз с учетом начальных условий (при t=0 x=x0=a): Подставив в соотношение (4.4) значения заданных величин, получим окончательно следующее уравнение движения груза:
Подставив в соотношение (4.4) значения заданных величин, получим окончательно следующее уравнение движения груза: