Пример решения задачи 3.2
Дано: m=40 кг, v0=10 м/с, t2=8 с, Р0=0, t3=12 с, Р1=250 Н, Р2=300/200 Н, α =30°, f=0, 1. Определить v1, v2, v3 и t1, t2, t3. Решение Покажем силы, действующие на тело (рис. 3.3): вес Построим график Р=Р(t) по заданным значениям Р0, Р1, Р2, Р3 (рис. 3.4) Рис. 3.4. 1. Для тела, принимаемого за материальную точку, составим уравнение, выражающее теорему об изменении количества движения в проекциях на ось Х для промежутка времени от 0 до t: mv1x - mvox = Σ S ix; где Σ S ix=Gt1 Проекция импульса переменной силы Р за t1 с: Spx= Этот интеграл определяется как площадь треугольника ОВМ на графике Р=Р(t): Spx= Учитывая, что сила трения скольжения F=fN=fG cosα, получаем уравнение (1) в следующем виде: mv1x-mv0x=-gt1 sinα -fg cosα t1+375, откуда v1x=v0x-gt1 sinα – fg cosα t1+ т.е. v1x=10-9, 81 таким образом, v1= v1x=2, 10 м/с. 2. Для определения скорости тела в момент времени t2 составим уравнение, выражающее теорему об изменении количества движения, для промежутка времени t2-t1: mv2x- mv1x= Σ Six где Σ Six=-G(t2-t1) Проекция импульса переменной силы Р за (t2-t1) с выражается площадью трапеции МВСL S на графике Р=Р(t): Spx= - Поэтому уравнение имеет вид mv2x-mv1x=-mg(t2- t1) sinα -fmg cosα (t2- t1)+1375, откуда v2x=v1x-g(t2- t1) sinα – fg cosα (t2- t1)+ =2, 10-9, 81 Таким образом, v2=v2x=7, 68 м/с. 3. Уравнение, выражающее теорему об изменении количества движения и составленное для промежутка времени t3-t2, дает возможность определить скорость тела v3 в момент t3: mv3x-mv2x= Σ Six где Σ Six=-G(t3-t2) Проекция импульса переменной силы Р за (t3-t2) с выражается площадью трапеции УDEK: Spx= тогда v3x=v2x-g(t3- t2) sinα – fg cosα (t3- t2)+ =7, 68-9, 81 Таким образом, v3=v3x=2, 15 м/с.
|

 , нормальную реакцию плоскости
, нормальную реакцию плоскости  , силу
, силу  и силу трения скольжения
и силу трения скольжения 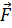 , направив её противоположно начальной скорости, т.е. вниз по наклонной плоскости.
, направив её противоположно начальной скорости, т.е. вниз по наклонной плоскости.
 - Ft1 + Spx.
- Ft1 + Spx.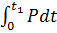 .
.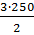 =375Н
=375Н  с
с ,
, - F(t2-t1) + Spx.
- F(t2-t1) + Spx. =1375 Н
=1375 Н 
 =
=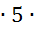 0, 5-0, 1
0, 5-0, 1  =2, 10-24, 52-4, 27+34, 38=7, 68 м/с.
=2, 10-24, 52-4, 27+34, 38=7, 68 м/с.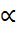 (t3-t2)+Spx.
(t3-t2)+Spx. =700 Н
=700 Н  =
= 0, 5-0, 1
0, 5-0, 1  =7, 68-19, 62-3, 41+17, 5=2, 15 м/с.
=7, 68-19, 62-3, 41+17, 5=2, 15 м/с.


