Пример решения задачи 3.4
Условие. Однородный каток В весом Q=4 кН и радиусом R и груз А весом Р=2 кН, соединенные гибкой нерастяжимой и невесомой нитью, помещены на шероховатую поверхность, наклоненную к горизонту под углом a=300 (рис. 3.9). Нить переброшена через невесомый блок О радиусом 30 см. К свободному концу нити приложена сила F, линейно зависящая от величины перемещения s: F=9, 0+0, 15× s (кН). Каток катится без скольжения; коэффициент трения скольжения груза о плоскость f=0, 1, момент сил сопротивления в подшипнике блока М=300 Н м. Определить скорость груза А, когда он переместится на величину s=3 м. В начальный момент система находилась в покое.
где T, T0 – кинетическая энергия системы соответственно в конечный и начальный моменты времени;
В рассматриваемой задаче система состоит из катка, груза, блока и нити. Система сил, действующих на систему, включает активные силы Q, P, F, реакции связей NA, NB, Fсц, Fтр, Rx, Ry и момент трения в блоке M. Найдем сумму работ всех внешних сил системы на соответствующих перемещениях точек их приложения:
Работы сил NА и NB равны нулю, так как направления этих сил составляют прямой угол с направлениями перемещений точек их приложения. Работа силы сцепления Fсц и работы реакций Rx и Rу равны нулю, так как эти силы приложены к неподвижным точкам. Работы сил F, Р, Q, Fтр и пары сил с моментом М определим следующим образом:
После суммирования получим
Рассматриваемая механическая система состоит из абсолютно твердых тел, соединенных идеальной нитью. Для таких систем с идеальными связями сумма работ всех внутренних сил равна нулю
Рассчитаем кинетическую энергию системы в начальном и конечном положениях. По условию задачи система в начальный момент находилась в покое, следовательно, ее кинетическая энергия в этот момент равна нулю T0=0. Кинетическая энергия груза А, движущегося поступательно, равна
где Кинетическая энергия катка В, совершающего плоское движение, равна
где vC – скорость центра масс С катка,
wВ – угловая скорость катка, Кинетическая энергия системы равна сумме кинетических энергий всех тел, входящих в нее:
Подставляя выражения (2) – (4) в формулу (1), выражающую теорему об изменении кинетической энергии системы, получим
откуда искомая скорость груза А, в момент, когда он переместится на расстояние 3 м, равна
Список литературы Основная литература 1. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов / 19-е изд., стер.- М.: Высш.шк., 2009.- 416 с.: ил. 2. Мещерский И.В. Задачи по теоретической механике: Учебное пособие, 50-е изд., стер. / Под ред. В.А. Пальмова, Д.Р. Меркина.- СПб.: Издательство «Лань», 2010.-448 с.: ил.
Дополнительная литература 1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах: Учеб. пособ. – М.: Политехника, 1995 – 670с. 2. Бутенин Н.В., Лунц Я.П., Меркин Д.Р. Курс теоретической механики. – М., 1985. Т. 1, 2. 3. Гернет М.М. Курс теоретической механики: Учеб. для вузов. – М.: Высш. шк., 1987. - 344 с. 4. Голубев Ю.Ф. Основы теоретической механики: Учеб. для вузов. – М.: Изд-во МГУ, 1992. - 524 с. 5. Попов М.В. Теоретическая механика: Краткий курс: Учеб. для вузов. – М.: Наука, 1986. – 336 с. 6. Сборник задач по теоретической механике: Учеб. пособие для студентов вузов / Будник Ф.Г., Зингерман Ю.М., Зеленский Е.И.; под ре. Кельзона А.С. – Высш. шк., 1987. – 176 с. 7. Никитин Е.М. Теоретическая механика для техникумов.- 12-е изд., испр.- М.: Наука. Гл.ред.физ.-мат.лит., 1988.- 336 с.
Задания и методические указания к выполнению контрольных работ по дисциплине «Теоретическая механика»
Подписано в печать. Формат 60х84/16. Бумага для множ. аппаратов. Печать плоская. Усл. печ. л. ____. Уч.- изд. л.___. Тираж____ экз. Заказ____ ФГАОУ ВПО «Российский государственный профессионально-педагогический университет, Екатеринбург, ул. Машиностроителей, 11.
|

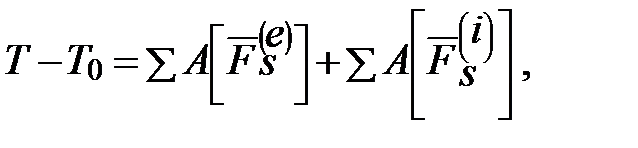 (1)
(1)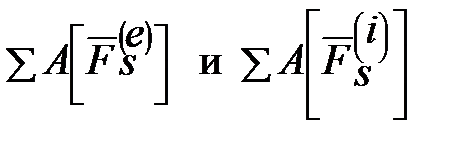 – суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.
– суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.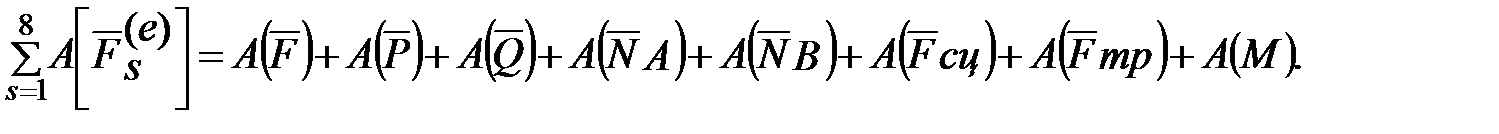
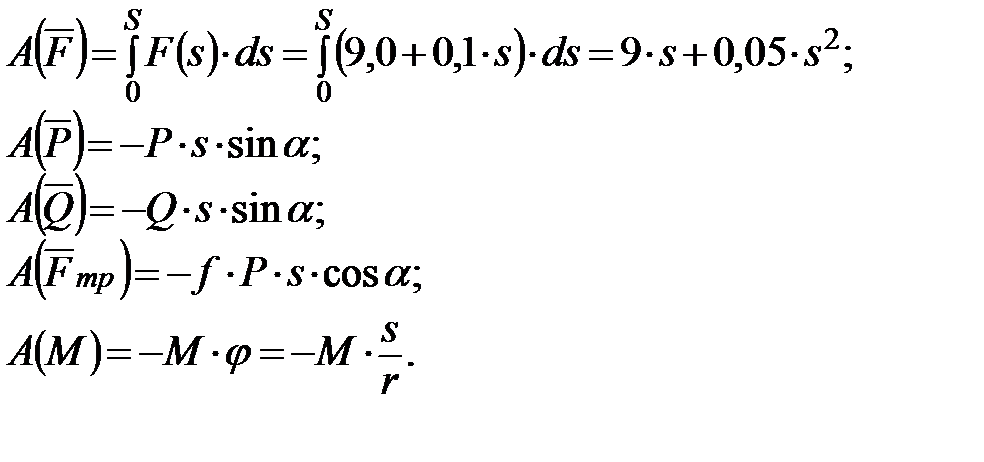
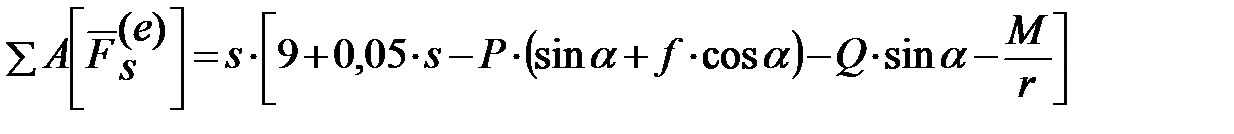 . (2)
. (2) . (3)
. (3) ,
,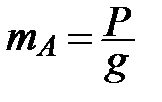 – масса груза А;
– масса груза А; 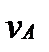 – скорость груза.
– скорость груза.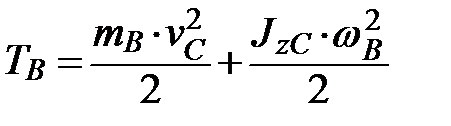 ,
, – масса катка В;
– масса катка В; ;
;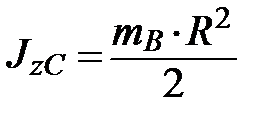 – момент инерции катка относительно оси, проходящей через его центр масс;
– момент инерции катка относительно оси, проходящей через его центр масс;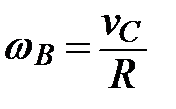 .
.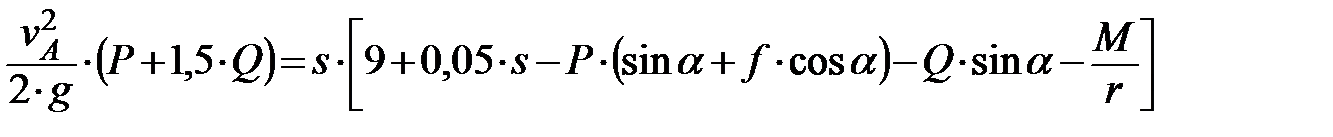 (4)
(4)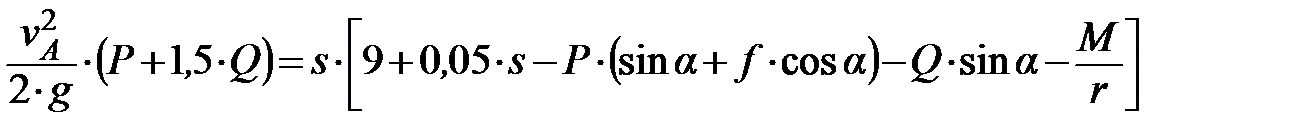 ,
,



