Условие. Точка М движется по ободу диска радиусом R=20 см согласно закону s = АМ = 6 t sin(pt/3). Диск вращается вокруг неподвижной оси О1О2, лежащей в плоскости диска, в направлении, указанном стрелкой, с постоянной
угловой скоростью w=0, 5 рад/с. Определить абсолютную скорость точки М в момент времени t 1 =5 с (рис.2.4).

Решение. В данной задаче относительное движение точки – движение по ободу диска относительной системы отсчета, связанной с диском; переносное движение – вращение вместе с диском вокруг неподвижной оси; абсолютное движение – движение точки относительно неподвижной оси.
Определим параметры относительного движения точки:
а) положение точки М в заданный момент времени t=5 с:

Знак минус означает, что точка М в рассматриваемый момент времени находится в области отрицательных значений дуговой координаты s;
б) определим центральный угол a и отрезок MN: 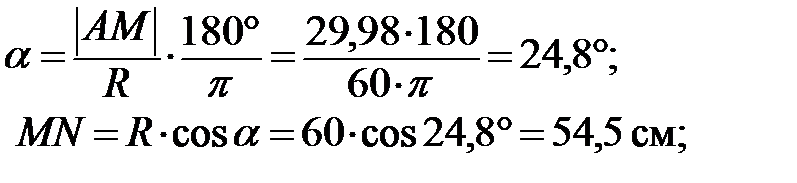
в) найдем проекцию относительной скорости  точки М на касательную в данный момент времени (рис. 2.5).
точки М на касательную в данный момент времени (рис. 2.5).
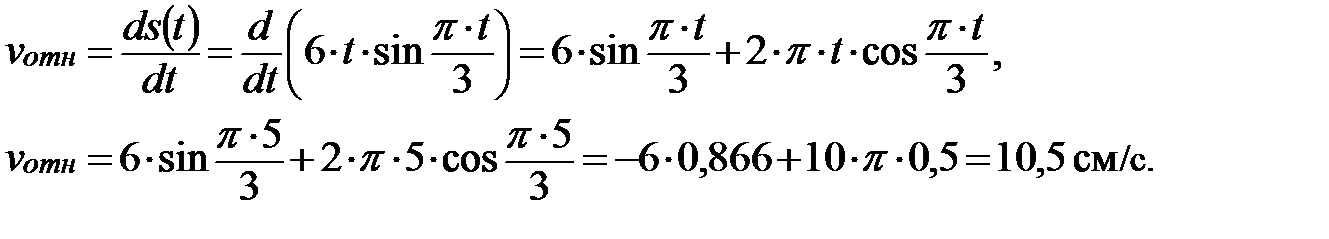

Определим модуль переносной скорости точки М как вращательной скорости той точки диска, где в данное мгновение находится точка М
 .
.
Вектор переносной скорости перпендикулярен плоскости диска и направлен в сторону его вращения.
Модуль абсолютной скорости точки М (рис. 2.5.) найдем по формуле: 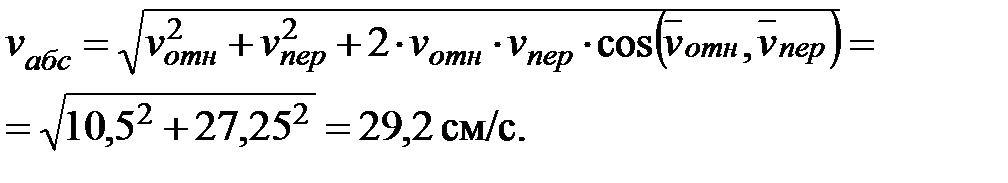
Вектор абсолютной скорости направлен по диагонали прямоугольника, построенного на относительной и переносной скоростях как сторонах.
Абсолютное ускорение  точки М равно (рис. 2.6) геометрической сумме относительного
точки М равно (рис. 2.6) геометрической сумме относительного  отн, переносного
отн, переносного  пер и кориолисова
пер и кориолисова  кор ускорений:
кор ускорений:  абс =
абс =  отн +
отн +  пер +
пер +  кор, или с учетом условий задачи в развернутом виде
кор, или с учетом условий задачи в развернутом виде  абс =
абс = 
 отн +
отн + 
 отн +
отн + 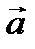
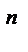 пер +
пер +  кор
кор
где при t1=5с касательное ускорение в относительном движении:
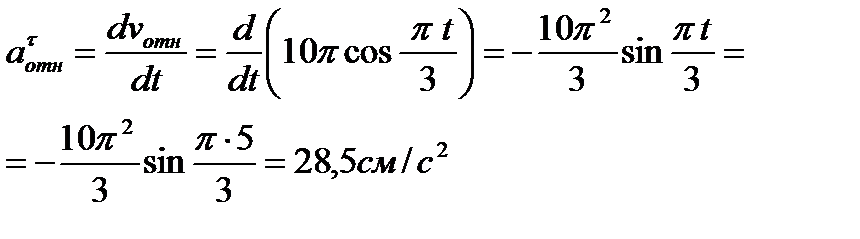
;
нормальное ускорение в относительном движении:

 отн =
отн =  ;
;
нормальное ускорение в переносном движении:

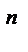 пер =
пер =  ;
;
кориолисово ускорение:
 кор =
кор =  .
.
Положительный знак 
 отн показывает, что вектор
отн показывает, что вектор 
 отн направлен в сторону положительных значений S; вектор
отн направлен в сторону положительных значений S; вектор 
 отн направлен по нормали к траектории движения точки в относительном движении, т.е. по нормали к окружности радиусом MN к её центру, вектор
отн направлен по нормали к траектории движения точки в относительном движении, т.е. по нормали к окружности радиусом MN к её центру, вектор  кор направлен согласно правилу векторного произведения векторов
кор направлен согласно правилу векторного произведения векторов  и
и  отн (рис. 2.6)
отн (рис. 2.6)
Модуль абсолютного ускорения точки М находим способом проекции на оси х, у и z (рис. 2.6):
 абс x =
абс x = 
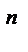 пер +
пер + 
 отн cos
отн cos  -
- 
 отн sin
отн sin  =13, 6 + 4, 1cos 24, 8
=13, 6 + 4, 1cos 24, 8 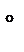 – - sin 24, 8
– - sin 24, 8 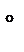 = 5, 37 см/с2
= 5, 37 см/с2
 абс y = -
абс y = - 
 отн sin
отн sin  -
- 
 отн cos
отн cos  = 4, 1sin 24, 8
= 4, 1sin 24, 8 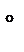 – 28, 5cos24, 8
– 28, 5cos24, 8 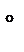 = = -27, 6 см/с2
= = -27, 6 см/с2  абс z =
абс z =  кор = 6, 6 см/с2
кор = 6, 6 см/с2
 абс =
абс =  см/с2
см/с2
Рис.2.6.
Направление вектора  абс определяется его углами с осями координат:
абс определяется его углами с осями координат:
( абс ^,
абс ^,  ) = аrс cos
) = аrс cos  = абс cos
= абс cos  = 79, 3
= 79, 3 
( абс ^,
абс ^,  ) = аrс cos
) = аrс cos  = абс cos
= абс cos  = 162, 7
= 162, 7 
( абс ^,
абс ^,  ) = аrс cos
) = аrс cos 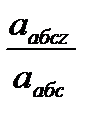 = абс cos
= абс cos  = 76, 8
= 76, 8 

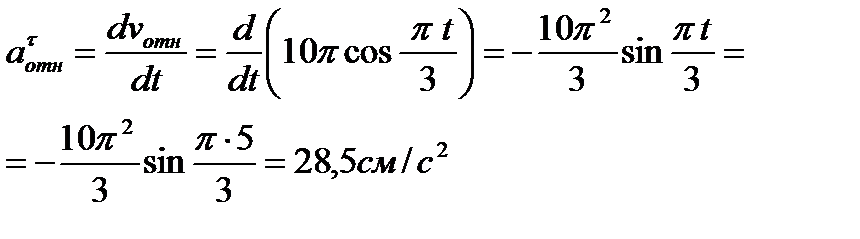 ;
;


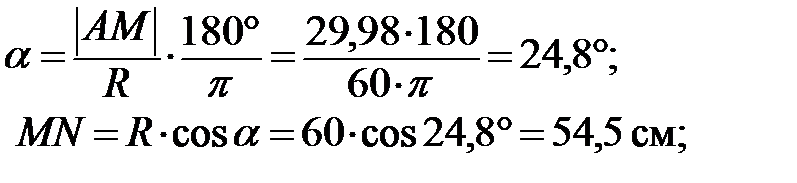
 точки М на касательную в данный момент времени (рис. 2.5).
точки М на касательную в данный момент времени (рис. 2.5).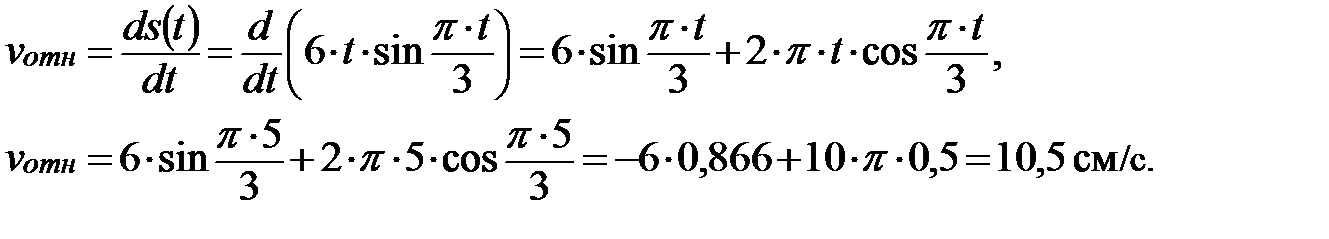
 .
.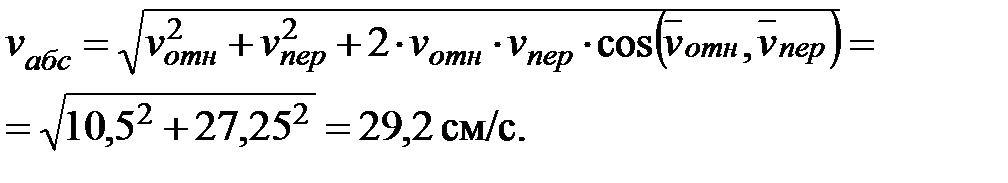
 точки М равно (рис. 2.6) геометрической сумме относительного
точки М равно (рис. 2.6) геометрической сумме относительного  отн, переносного
отн, переносного  абс =
абс =  отн +
отн +  пер +
пер +  кор, или с учетом условий задачи в развернутом виде
кор, или с учетом условий задачи в развернутом виде  абс =
абс = 
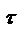 отн +
отн + 
 отн +
отн + 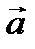
 пер +
пер +  кор
кор
 ;
; ;
; кор =
кор =  .
. отн показывает, что вектор
отн показывает, что вектор  и
и  отн (рис. 2.6)
отн (рис. 2.6) -
-  – - sin 24, 8
– - sin 24, 8  кор = 6, 6 см/с2
кор = 6, 6 см/с2 см/с2
см/с2
 ) = аrс cos
) = аrс cos  = абс cos
= абс cos  = 79, 3
= 79, 3  ) = аrс cos
) = аrс cos  = абс cos
= абс cos  = 162, 7
= 162, 7  ) = аrс cos
) = аrс cos  = абс cos
= абс cos  = 76, 8
= 76, 8 


