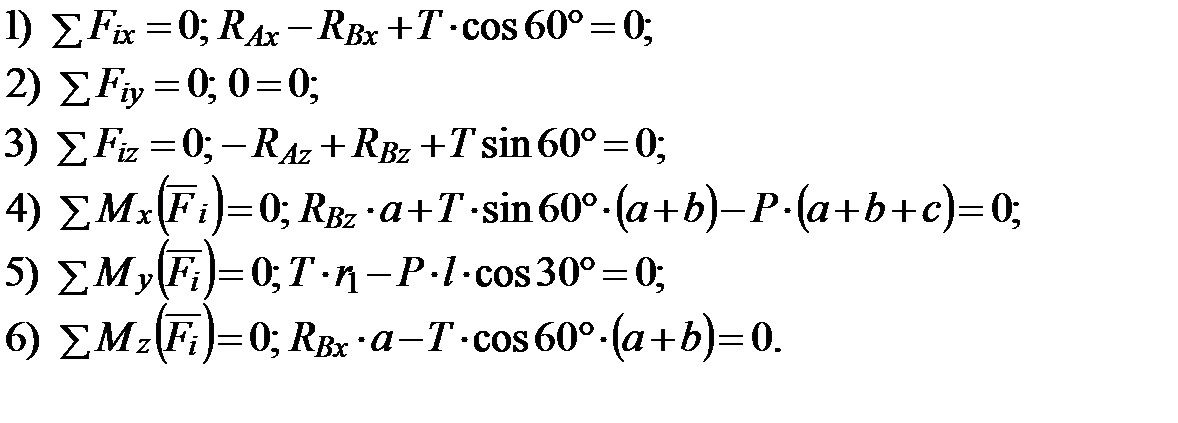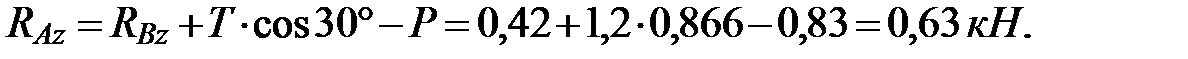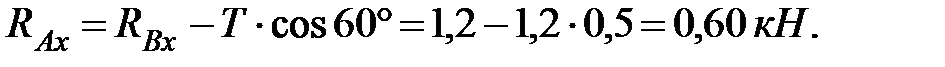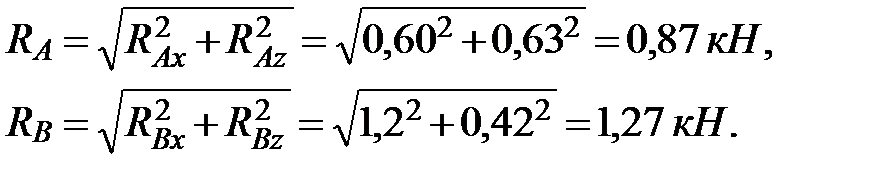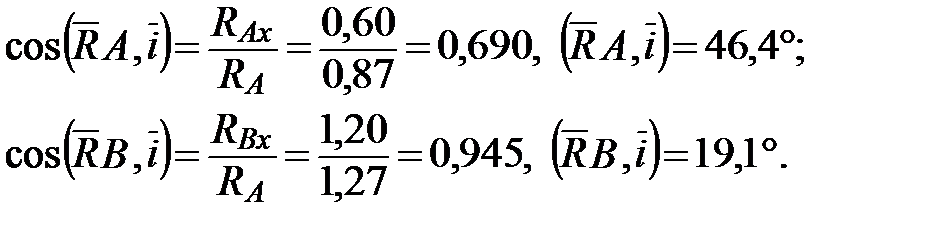Пример решения задачи 1.2

Условие. На горизонтальный вал насажено колесо радиусом r₁ = 12 см и прикреплен перпендикулярно оси вала рычаг СD длиной l = 20 см, образующий с горизон­тальной плоскостью угол α ₂=30°. Веревка, намотанная на колесо и натягиваемая грузом F=1, 2 кН, сходит с колеса по касательной, наклоненной под углом α ₁=60° к горизонту. Пренебрегая весом вала, колеса, рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В, если a = b = c = 1, 8 м (см. рис. 1.3, схема 10).

Решение. К валу кроме силы Р, действующей на рычаг СD, приложена реакция веревки (сила натяжения) T, численно равная силе тяжести груза F, так как по условию задачи трения в блоке нет (рис. 1.4, а). Направлена эта реакция вдоль веревки в ту сторону, куда веревка тянет блок. Реакции подшипников R_A и R_B, расположенные в плоскостях, перпендикулярных оси Аy, разложим на составляющие по осям координат R_Ax, R_Az, R_Bx и R_Bz. Направление реакций выбирается произвольно.

Рис. 1.4. Пример решения задачи на статическое равновесие пространственной системы сил

 

Для составления уравнений равновесия рассмотрим вид с положительного направления координатных осей, например с оси Ay (рис. 1.4, б).

Условия равновесия пространственной системы сил:

Из последнего соотношения найдем

Из пятого соотношения определим

Из четвертого соотношения вычислим

Из третьего соотношения найдем

Из первого соотношения найдем

Модули реакций подшипников:

Для определения направления реакции найдем угол между соответствующей реакцией и осью x:

2. КОНТРОЛЬНАЯ РАБОТА ПО РАЗДЕЛУ «КИНЕМАТИКА»