ЗАДАЧА 3. Для заданных сечений, состоящих из прокатных профилей и полосы b×h, определить положение центра тяжести
Для заданных сечений, состоящих из прокатных профилей и полосы b× h, определить положение центра тяжести.
ПРИМЕР 3. Определить координаты центра тяжести сечения. Сечение состоит из двутавра № 18, швеллера № 18 и пластины 200*60 (рисунок-6)
Рисунок - 6
1 Разобьем сечение на профили проката. Оно состоит из двутавра № 18, швеллера № 18 и пластины 200*60. обозначим их 1, 2, 3. 2 Укажем центры тяжести каждого профиля, используя таблицу приложения, и обозначим их С1, С2, С3, проведем через них оси Х1, Х2, Х3. 3 Выберем систему координатных осей. Ось Y совместим с осью симметрии, а ось Х проведем через центр тяжести двутавра. 4 Определим центр тяжести всего сечения. Так как ось Y совпадает с осью симметрии, то она проходит через центр тяжести сечения, потому Хс=0. Координату Yс определим по формуле:
Пользуясь таблицами ГОСТ 8239-89, ГОСТ 8240-89, ГОСТ 8510-86, ГОСТ 8509-86, определим координаты центров тяжести А1 = 20, 7 см2 А2 = 23, 4 см2 y 2 = 0 А3 = 20*6 = 120 см2 Координата у2 равна нулю, так как ось Х проходит через центр тяжести двутавра. Подставим полученные значения в формулу для определения уС:
1 Укажем центр тяжести сечения на рисунке и обозначим его буквой С. Покажем расстояние уС = -7, 82 см от оси Х до точки С. 2 Определим расстояние между точками С и С1, С и С2, С и С3, обозначим их а1, а2, а3: а1 = у1 + уС = 7, 57 + 7, 82 = 15, 39 см а2 = уС = 7, 82 см а1 = у3 - уС = 12 - 7, 82 = 4, 18 см 3 Выполним проверку. Для этого ось Х проведем по нижнему краю пластины. Ось Y оставим, как в первом решении. Формулы для определения хС и уС не изменятся: хС = 0, Площади профилей останутся такими же, а координаты центров тяжести двутавра, швеллера и пластины изменятся. А1 = 20, 7 см2 А2 = 23, 4 см2 А3 = 20*6 = 120 см2 Находим координату центра тяжести:
По найденным координатам хС и уС наносим на рисунок точку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Сумма координат уС, найденных при первом и втором решении: 7, 82 + 7, 18 = 15 см Это равно расстоянию между осями Х при первом и втором решении: 18/2 + 6 = 15 см.
ЗАДАЧА 4 По оси ступенчатого бруса приложены силы
ПРИМЕР 4 Для данного ступенчатого бруса построить эпюры продольных сил и нормальных напряжений. Определить абсолютное удлинение (укорочение) бруса (рисунок 7)
Дано:
 
    

Рисунок - 7
Решение 1 Проводим ось Z в сторону свободного конца бруса и определяем реакцию заделки
2 Разбиваем брус на участки, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние силы. На каждом из участков проводим характерные сечения 1-1, 2-2, 3-3. С помощью метода сечений определяем продольные силы на каждом из участков бруса: мысленно рассекаем брус в пределах первого участка сечения 1-1, отбрасываем верхнюю часть бруса и заменяем ее действие продольной силой N1 (рисунок 7) для оставшейся части составляем уравнение равновесия:
Аналогично находим N2 и N3:
сечение 2-2 (рисунок 7)
сечение 3-3 (рисунок 7)
По найденным значениям продольной силы строим соответствующую эпюру. Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем отрицательные значения N, соответствующие сжатому участку, а правее – положительные значения N, соответствующие растянутому участку (рисунок - 7). Определяем нормальные напряжения в характерных сечениях бруса по формуле:
Строим соответствующую найденным значениям эпюру σ (рисунок - 7)
4 Определяем абсолютное удлинение бруса. В соответствии с законом Гука:
где Е=2, 1*105 МПа – модуль продольной упругости для стали.
Складывая удлинение участков, получим:
Учитывая, что I м=103мм, будем иметь:
Таким образом, абсолютное удлинение бруса ЗАДАЧА 5 По данным задачи 2 для двухопорной балки построить эпоры поперечных сил Qу и изгибающих моментов Мх. Подобрать сечение стального двутавра, приняв [σ ] = 160 МПа.
ПРИМЕР 5 Для двухопорной балки построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать сечение стального двутавра, приняв [σ ] = 160 МПа.
Дано: F1=24 kH; F2=36 кН; m1=18 кНм; m2=24 кНм;
Рисунок - 8
Решение 1 Составляем уравнение равновесия параллельной системы сил, из которых определяем опорные реакции балки:
 (6) (6)
Из уравнения (6) находим RAУ:
Из уравнения (5) находим В:
Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось У:
то есть реакции определены верно.
2 Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначим цифрами 1, 2, 3, 4 (рисунок 8 а)
Q1=Q2лев=F1=24 кН; Q2прав=Q3лев=F1+RАУ=24-13=11 кН; Q32прав=Q4=F1+RАУ-F2= -RВУ= -25 кН.
По найденным значениям строим эпюру, поперечных сил Q (рисунок 8 б).
3 Аналогично определяем значения изгибающего момента М в характерных сечениях балки: М1=0; М2лев=F1*2.0=48 кНм М2прав=М2лев+m1=48+18=66 кНм; М3=F1*5.0+m1+RАУ*3, 0=120+18-39=99 кНм; М4=m2=24 кНм.
По найденным значениям строим эпюру изгибающих моментов М (рисунок 8 в).
4 По эпюре изгибающих моментов определяем положение опасного сечения балки (сечение, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение 3, где М3=Мmaх=99 кНм. Из условия прочности балки на изгиб
В соответствии с ГОСТ 8239-89 принимаем сечение из стального двутавра № 33 с Wх=597 см3. Имеем перенапряжение:

что находится в разрешенных пределах (менее 5%).
Ответ: сечение балки двутавр № 33. V. Список литературы 1. Аркуша. А. И. Техническая механика. Теоретическая механика и сопротивление материалов: Учеб. для средних спец. учеб. заведений/А. И. Аркуша. — 4-е изд., испр. — М.: Высшая. школа., 2002. — 352 с.: 2. Аркуша А.И. Руководство к решению задач по теоретической механике. – М.: Высшая школа, 2002
|




 7, 57 см
7, 57 см -12 см
-12 см -7, 82 см
-7, 82 см
 22, 57 см
22, 57 см 15 см
15 см 3 см
3 см 7, 18 см
7, 18 см и
и 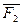 . Необходимо построить эпюры продольных сил и нормальных напряжений, определить абсолютную деформацию бруса. Принять Е = 2, 1 * 105 МПа.
. Необходимо построить эпюры продольных сил и нормальных напряжений, определить абсолютную деформацию бруса. Принять Е = 2, 1 * 105 МПа.

 ,
, 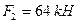 ,
,  м,
м,  м,
м,  м, А=3, 2 см 2, Е=2, 1*105 МПа
м, А=3, 2 см 2, Е=2, 1*105 МПа

 :
:

 ;
; .
.
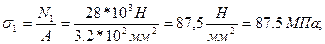

 .
.



 (87, 5*2, 4+43, 75*2, 2-112, 5*2, 0)=0, 39 мм.
(87, 5*2, 4+43, 75*2, 2-112, 5*2, 0)=0, 39 мм. = 0, 39 мм.
= 0, 39 мм.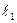 =2.0 м;
=2.0 м;  м;
м;  м.
м.




 вычисляем необходимый осевой момент сопротивления:
вычисляем необходимый осевой момент сопротивления: .
.



