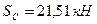ЗАДАЧИ К КОНТРОЛЬНОЙ РАБОТЕ
ЗАДАЧА1
Определить аналитическим и графическим способами усилия в стержнях АВ и ВС заданной стержневой системы.
ПРИМЕР 1
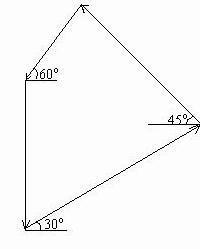
Определить аналитическим и графическим способами в стержнях АВ и ВС заданной стержневой системы (рисунок 1). Дано: F1 = 28 кН; F2 = 42 кН; α 1=450; α 2=600; α 3=300.
Определить: усилия
Рисунок -1
РЕШЕНИЕ 1 Аналитическое решение 1 Рассматриваем равновесие точки В, в которой сходятся все стержни и внешние силы (рисунок 1). 2 Отбрасываем связи АВ и ВС, заменяя их усилиями в стержнях
3 Выбираем систему координат таким образом, чтобы одна из осей совпадала с неизвестным усилием, например, с
Рисунок - 2
Из уравнения (2) находим усилие Sс:
Подставляем числовые значения:
Найденное значение Sс подставляем в уравнение (1) и находим из него значение SА:
SА= 42*0, 259+28*0, 707+21, 51*0, 259=36, 24 кН.
Окончательно SA =36, 24 кН, Sс=21, 51 кН; знаки указывают, что оба стержня растянуты.
2 Графическое решение Выбираем масштаб сил Из произвольно выбранной точки 0 откладываем отрезок, соответствующий величине и направлению силы
Рисунок - 3
Измеряя отрезки
Вычислим допущенную при графическом способе решения ошибку:
(Ошибка находится в пределах 2%).
Ответ: а) аналитическое решение:
б) графическое решение:
|
10
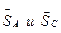
А. Обозначаем на схеме углы, образованные действующими силами с осью Х и составляем углы, образованные действующими силами с осью Х и составляем уравнения равновесия плоской системы сходящихся сил: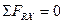
; F2cos 750+F1cos 450+Sccos 750-SА=0 (1);
; F2cos 150-F1cos 450-Sccos 150=0 (2).
, тогда силы 
будут откладываться отрезками 
; 
.
. Из конца этого отрезка откладываем отрезок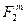 
. Так как условием равновесия сходящейся системы сил является замкнутость силового многоугольника, то из начала отрезка 
откладываем линию, параллельную вектору 
, а из конца отрезка 
. Точка их пересечения является вершиной силового многоугольника (рисунок 3).
и 
и, умножая их на масштаб находим значения SА и SС:
;
.
