Дифференциальное уравнение оси изогнутого брусаУчебно-методическое пособие к лабораторным занятиям
Составитель Шушарин Анатолий Васильевич
Редактор Л. Л. Шигорина
Подписано в печать 2. 02. 08. Формат 60 х 84 1/16. Тираж 200 экз. Заказ 4. Цена договорная
Отпечатано в Издательском центре ЧИПС 454111 Челябинск, ул. Цвиллинга, 56
Дифференциальное уравнение оси изогнутого бруса В результате изгиба балки ось становится криволинейной (см. рис. 11.1), центры поперечных сечений перемещаются от первоначальной прямой линии и поворачиваются на какой-то угол (рис. 11.1). За прогиб V принимают перемещение центра сечения перпендикулярно первоначальной оси. Для сечения К прогиб составит отрезок КК1.
Рис. 11.1 Для определения перемещений сечений балки пользуются дифференциальным уравнением изогнутой оси балки:
где Е - модуль продольной упругости, I - осевой момент инерции сечения,
М - изгибающий момент. В точке К1 проведем касательную к изогнутой оси балки, которая образует с осью Z угол, так как линии, образующие углы, перпендикулярны. Из высшей математики известно, что первая производная от функции равна тангенсу угла наклона касательной, т.е.
Для малых значений угла справедливо равенство:
|
, (11.1)
- вторая производная от прогиба,
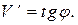
. Следовательно, первая производная от прогиба представляет собой угол поворота сечения.
