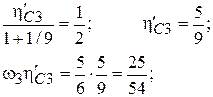Правило Верещагина
В 1925 году студент Московского института инженеров железнодорожного транспорта Верещагин предложил упрощение техники определения перемещений, используя интеграл Мора. Этот способ получил название способа перемножения эпюр или правила Верещагина. Пусть грузовая эпюра имеет сложное (нелинейное) очертание, а единичная - линейное (см. рис. 11.6). Интеграл Мора имеет вид:
При I = const и E = const их можно вынести за интеграл и принять пределы интегрирования, указанные на рисунке:
Из рисунка видно, что Тогда:
Рис. 11.6 Но Интеграл принимает вид:
т.е. статический момент площади грузовой эпюры моментов относительно оси Y. Тогда формула запишется:
Статический момент любой фигуры равен произведению площади на расстояние от оси до центра тяжести:
где
Из треугольника ОС1С2 имеем:
где
Поскольку к балке может быть приложено несколько нагрузок (внешние моменты, силы, распределенные нагрузки) в нескольких сечениях, то перемещения определяют для каждого участка балки. Поэтому, в общем случае формула Верещагина имеет вид:
Пример: Для балки, приведенной на рис. 2.16 определить прогиб в сечении В и угол поворота сечения С. Решение: Перерисуем балку и эпюру грузовых моментов (см. рис. 11.7). Вначале определим прогиб в сечении В, для чего к нему приложим единичную силу, направленную вверх, и построим эпюру моментов от нее. В силу симметрии реакции опор будут равны и направлены вниз. В сечении В момент равен:
Поскольку единичная сила безразмерна, то момент от нее имеет размерность длины. Участок ВС будет симметричным участку АВ, а на участке СД момент от единичной силы отсутствует. Согласно правила Верещагина:
Рис.11.7 В данном примере перемножаться будут эпюры участков АВ и ВС, так как на участке СД М1=0. На участке АВ сложно определить площадь эпюры и положение ее центра тяжести, поэтому эпюру разобьем на треугольник и сегмент. Для сегмента нужно знать высоту. Поэтому определим значение грузового момента для сечения Е, расположенного посредине участка АВ, т.е. на расстоянии 0, 5 м от опоры А. Будем рассматривать левую часть балки:
Высота сегмента равна 7, 5 - 2, 5 = 5кНм. Произведение
Площадь треугольника равна
На участке ВС грузовая эпюра представляет собой два треугольника, причем до сечения М площадь положительна, а от М до С - отрицательна. Определим длину участка ВМ. Обозначим его через z, тогда МС = 1 - z. Из подобных треугольников получим:
или
Тогда
Значение
или
откуда
Площадь
Прогиб в сечении В равен:
Знак " минус" показывает, что перемещение сечения В будет в обратную сторону, чем направление единичной силы, т.е. вниз. Для определения угла поворота сечения С приложим к нему единичный момент, направленный против часовой стрелки. Реакция в опоре А будет:
Строим эпюру моментов
Проводим наклонную прямую от Перемножим грузовую эпюру моментов и эпюру
Для треугольника:
На участке ВС для верхнего треугольника:
для нижнего треугольника:
Угол поворота сечения С равен:
Знак " плюс" свидетельствует, что сечение повернется в том же направлении, что и m = 1, т.е. против часовой стрелки.
|

 .
.
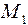 =ztg.
=ztg.

 =d - площадь заштрихованной части эпюры
=d - площадь заштрихованной части эпюры  .
.

 ,
, - площадь грузовой эпюры
- площадь грузовой эпюры  - расстояние до центра тяжести.
- расстояние до центра тяжести.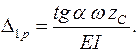

 - значение момента от единичной нагрузки под центром тяжести грузовой эпюры.
- значение момента от единичной нагрузки под центром тяжести грузовой эпюры.

 .
.
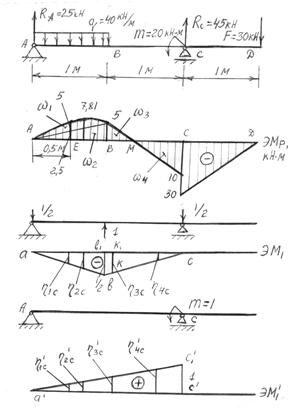
 .
. для разных фигур дано в некоторых учебниках (П.А. Степин) и справочниках по сопротивлению материалов. В случае их отсутствия перемножение можно осуществить самим. Так для сегмента площадь равна 2/3fl, где f - высота, f = 5; l - длина, l = 1 (размерности писать не будем). Центр тяжести сегмента посредине, т.е. на расстоянии 0, 5, где на единичной эпюре
для разных фигур дано в некоторых учебниках (П.А. Степин) и справочниках по сопротивлению материалов. В случае их отсутствия перемножение можно осуществить самим. Так для сегмента площадь равна 2/3fl, где f - высота, f = 5; l - длина, l = 1 (размерности писать не будем). Центр тяжести сегмента посредине, т.е. на расстоянии 0, 5, где на единичной эпюре  = -1/4. Итого, для сегмента получим:
= -1/4. Итого, для сегмента получим: .
. . Центр тяжести треугольника находится на расстоянии 2/3 от вершины, т.е.
. Центр тяжести треугольника находится на расстоянии 2/3 от вершины, т.е.


 участок
участок 
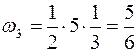 и центр тяжести на 1/9 от сечения В.
и центр тяжести на 1/9 от сечения В. определится из подобия треугольников сbb1 и ckk1.
определится из подобия треугольников сbb1 и ckk1.
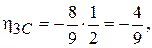

 и центр тяжести расположен на расстоянии
и центр тяжести расположен на расстоянии  от сечения С, поэтому:
от сечения С, поэтому:

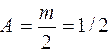 .
.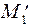 от единичного момента. В точке С изгибающий момент равен:
от единичного момента. В точке С изгибающий момент равен:
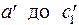 . На участке СД момент равен нулю.
. На участке СД момент равен нулю. а значение
а значение  определим из подобий треугольников:
определим из подобий треугольников: