Пусть балка нагружается двумя силами. Рассмотрим два состояния: 1) балка нагружается сначала силой 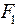 , а затем - силой
, а затем - силой 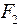 ; 2) балка нагружается сначала силой
; 2) балка нагружается сначала силой 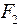 , а затем - силой
, а затем - силой 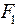 (см. рис. 11.3).
(см. рис. 11.3).
I состояние II состояние
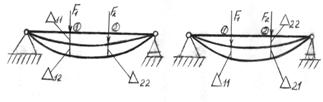
Рис. 11.3
Рассмотрим I состояние. Вначале к сечению 1 прикладывается сила 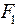 , в результате чего центр сечения 1 переместится на величину
, в результате чего центр сечения 1 переместится на величину  . Здесь первый индекс означает, что перемещается сечение 1, второй индекс - от действия силы
. Здесь первый индекс означает, что перемещается сечение 1, второй индекс - от действия силы 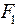 , в направлении ее действия. После приложим силу
, в направлении ее действия. После приложим силу 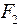 в сечении 2. В результате ее действия сечение 2 переместится на величину
в сечении 2. В результате ее действия сечение 2 переместится на величину  , а сечение 1 -
, а сечение 1 - 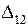 .
.
Определим работу, совершаемую силами 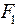 и
и 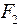 . При нагружении только силой
. При нагружении только силой 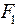 , работа равна:
, работа равна:
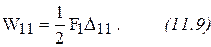
Число 1/2 взято потому, что сила 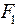 постепенно увеличивается от нуля до конечного значения и с увеличением силы растет перемещение. Аналогично:
постепенно увеличивается от нуля до конечного значения и с увеличением силы растет перемещение. Аналогично:
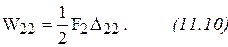
Но при нагружении силой 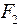 переместится и сечение 1, а, следовательно, сила
переместится и сечение 1, а, следовательно, сила 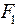 совершит путь
совершит путь 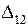 . Поскольку сила
. Поскольку сила 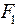 в данном перемещении постоянна, то выполняемая ею работа равна:
в данном перемещении постоянна, то выполняемая ею работа равна:

Во II состоянии  будут такими же, как и в I состоянии. Определим работу
будут такими же, как и в I состоянии. Определим работу 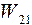 :
:
 .
.
Работа сил 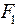 и
и 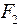 , совершаемая при I и II состояниях должна быть равна, поэтому:
, совершаемая при I и II состояниях должна быть равна, поэтому:
 =
= 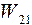
или
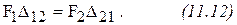
" Работа сил первого состояния на перемещение второго состояния равна работе сил второго состояния на перемещение первого состояния" (Теорема Бетти).
Если примем 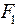 =
= 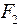 =1 (без размерности), то получим теорему о взаимности перемещений (теорему Максвелла):
=1 (без размерности), то получим теорему о взаимности перемещений (теорему Максвелла):

где  - перемещения, вызываемые единичными силами.
- перемещения, вызываемые единичными силами.
" Перемещения точки приложения единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки приложения второй единичной силы по направлению последней, вызванному действием первой единичной силы".

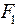 , а затем - силой
, а затем - силой 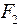 ; 2) балка нагружается сначала силой
; 2) балка нагружается сначала силой 
 . Здесь первый индекс означает, что перемещается сечение 1, второй индекс - от действия силы
. Здесь первый индекс означает, что перемещается сечение 1, второй индекс - от действия силы  , а сечение 1 -
, а сечение 1 - 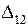 .
.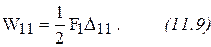
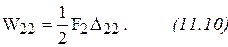

 будут такими же, как и в I состоянии. Определим работу
будут такими же, как и в I состоянии. Определим работу 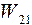 :
: .
. =
= 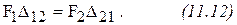

 - перемещения, вызываемые единичными силами.
- перемещения, вызываемые единичными силами.


