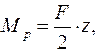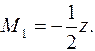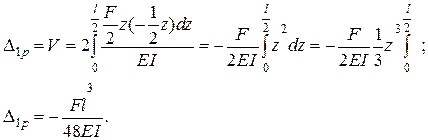Интеграл Мора для определения перемещений
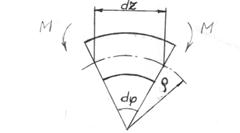
Определим потенциальную энергию бруса при чистом изгибе. Рассмотрим бесконечно малый отрезок балки длиной dz (см. рис. 11.4). Под действием момента он изогнется и радиус кривизны составит, а крайние сечения составят угол d.
Рис. 11.4 Из теоретической механики известно, что работа, совершаемая моментом, равна произведению момента на угол поворота:
где Множитель 1/2 берется потому, что с возрастанием момента М прямо пропорционально возрастает угол d, т.е. момент - не постоянная величина, он изменяется от нуля до конечного значения М. Из рис.11.4 видно:
Тогда, подставив
По формуле (10.2) имеем: 1/ где Е - модуль продольной упругости, I - осевой момент инерции сечения. Подставив в формулу (11.15), получим:
Для определения потенциальной энергии балки необходимо взять интеграл по ее длине:
Если пренебречь перемещениями от поперечной силы, то от силы
а от силы
Пусть к балке приложены силы
Согласно закона сохранения энергии, потенциальная энергия равна совершаемой работе: W = U; W11 = U11; W2 2= U22. Поэтому из формул (11.11) и (11.17) следует:
Как известно, если работу совершает сила, то она равна произведению силы на перемещение, а если момент - произведению момента на угол поворота. Поэтому для первого случая:
для второго:
При нагружении балки силой
Из формулы (11.19) следует, что если где М1 - момент от единичной силы,
Поскольку к балке может быть приложена различная нагрузка, то формулу можно записать следующим образом (формула Мора):
где М1 - момент от единичной силы или единичного момента, приложенных в точке, где следует определить перемещение, Мp - момент от обобщенной нагрузки. Используя формулу (11.20), можно определять перемещения в любой точке. Для этого в определяемой точке прикладывается единичная сила, если определяется прогиб, или единичный момент, если определяется угол поворота. Если знак у Пример: Определить прогиб посредине пролета для двухопорной шарнирной балки, нагруженной силой F (см. рис. 11.5).
Рис.11.5 Для определения прогиба в точке С, приложим единичную силу и направим ее вверх. Определим моменты от нагрузки:
момент от единичной силы:
Поскольку задача симметричная, то интеграл формулы Мора можно определять от 0 до l /2, умножив на 2:
Эта формула используется в лабораторной работе № 4.
|

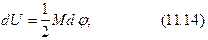
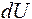 - потенциальная энергия отрезка dz балки.
- потенциальная энергия отрезка dz балки.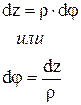
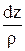 вместо
вместо 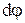 в формулу (11.14), получим:
в формулу (11.14), получим:
 =M/EI,
=M/EI,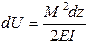 ,
,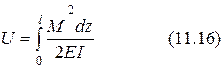
 в сечениях балки будут возникать моменты
в сечениях балки будут возникать моменты 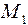 . Тогда потенциальная энергия будет равна:
. Тогда потенциальная энергия будет равна: ,
,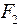 :
: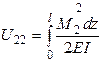 .
.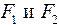 , тогда потенциальная энергия равна:
, тогда потенциальная энергия равна:
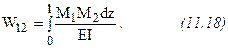
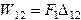 ,
,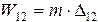 .
.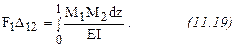

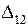 - перемещение в точке приложения единичной силы от силы
- перемещение в точке приложения единичной силы от силы 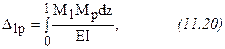
 - перемещение от обобщенной нагрузки,
- перемещение от обобщенной нагрузки,