 Поворот тела на некоторый угол
Поворот тела на некоторый угол  можно задать в виде отрезка длина которого
можно задать в виде отрезка длина которого  , а направление совпадает с осью вращения и определяется правилом правого винта: Направление должно быть таким, чтобы глядя вдоль него, мы видели поворот совершающийся по часовой стрелке.
, а направление совпадает с осью вращения и определяется правилом правого винта: Направление должно быть таким, чтобы глядя вдоль него, мы видели поворот совершающийся по часовой стрелке.
 При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота
При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота 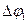 и
и  (вокруг разных осей, оси
(вокруг разных осей, оси 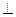 в данном случае) обуславливают как видно из рис., такое же перемещение,
в данном случае) обуславливают как видно из рис., такое же перемещение,  любой точки тела, как и поворот
любой точки тела, как и поворот  получаемый из
получаемый из 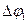 и
и  сложением о правилу параллелограмма. Значит очень малые повороты можно рассматривать как векторы. Направление вектора поворота
сложением о правилу параллелограмма. Значит очень малые повороты можно рассматривать как векторы. Направление вектора поворота  , связывается с направлением вращения тела, следовательно
, связывается с направлением вращения тела, следовательно  не является истинным вектором, а является псевдовектором.
не является истинным вектором, а является псевдовектором.
Векторная величина
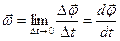
называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль
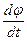
, если

— равномерное вращение
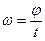
, для равномерного движения

-угол поворота в единицу времени.
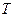
период вращения

число оборотов
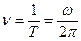
, а
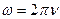
.
 Понятия
Понятия 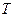 и
и  можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.
можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.
Вектор  может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за
может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за 
 получает приращение
получает приращение  то изменение угловой скорости со временем характеризуется угловым ускорением
то изменение угловой скорости со временем характеризуется угловым ускорением

 — тоже псевдовектор.
— тоже псевдовектор.
Точки вращающегося тела имеют разные линейные скорости, которые определяют  и
и  . Если за
. Если за  тело повернулось на
тело повернулось на  , то
, то 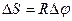 . Линейная скорость точки
. Линейная скорость точки 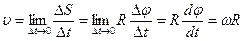 ; т.е.
; т.е.  .
.
Найдем связь между векторами  и
и  . Положение для модулей точки определяет
. Положение для модулей точки определяет 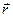 . Из рис. видно, что
. Из рис. видно, что 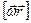 совпадает с
совпадает с  по направлению, модуль
по направлению, модуль 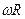 равен
равен 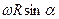 .
.
Модуль нормального ускорения точек  или через
или через 
 .
.
Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:
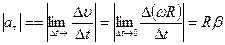 ;
;  -модуль угловой скорости, т.е
-модуль угловой скорости, т.е  .
.
Т.о. нормальное и тангенциальное ускорение растут пропорционально  .
.
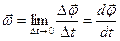 называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль
называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль 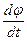 , если
, если  — равномерное вращение
— равномерное вращение 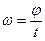 , для равномерного движения
, для равномерного движения  -угол поворота в единицу времени.
-угол поворота в единицу времени. 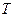 период вращения
период вращения  число оборотов
число оборотов 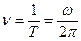 , а
, а 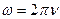 .
.

 Поворот тела на некоторый угол
Поворот тела на некоторый угол  можно задать в виде отрезка длина которого
можно задать в виде отрезка длина которого  При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота
При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота 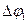 и
и  (вокруг разных осей, оси
(вокруг разных осей, оси 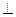 в данном случае) обуславливают как видно из рис., такое же перемещение,
в данном случае) обуславливают как видно из рис., такое же перемещение,  любой точки тела, как и поворот
любой точки тела, как и поворот  получаемый из
получаемый из  , связывается с направлением вращения тела, следовательно
, связывается с направлением вращения тела, следовательно  не является истинным вектором, а является псевдовектором.
не является истинным вектором, а является псевдовектором.
 Понятия
Понятия  можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.
можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение. может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за
может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за 
 то изменение угловой скорости со временем характеризуется угловым ускорением
то изменение угловой скорости со временем характеризуется угловым ускорением
 — тоже псевдовектор.
— тоже псевдовектор. . Если за
. Если за 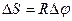 . Линейная скорость точки
. Линейная скорость точки 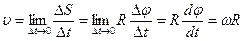 ; т.е.
; т.е.  .
. и
и 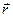 . Из рис. видно, что
. Из рис. видно, что 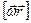 совпадает с
совпадает с 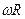 равен
равен 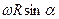 .
. или через
или через  .
.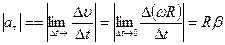 ;
;  -модуль угловой скорости, т.е
-модуль угловой скорости, т.е  .
.


