Кроме энергии и импульса существует ещё Одина физическая величина. С которой связан закон сохранения — это момент импульса. Моментом импульса частицы 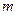 относительно точки О называется вектор
относительно точки О называется вектор  равный
равный  ,
, 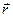 -радиус; -импульс.
-радиус; -импульс.
Т.е.  является??? вектором. Его направление выбрано так, что вращение вокруг О в направлении
является??? вектором. Его направление выбрано так, что вращение вокруг О в направлении  и вектор
и вектор  образует правовинтовую систему. Модуль
образует правовинтовую систему. Модуль 
 угол между
угол между 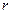 и
и 
 плечо вектора
плечо вектора  относительно О.
относительно О.
Найдем с какой величиной связано изменение вектора  во времени:
во времени:

 .
.
 Т.к т.о неподвижна, то
Т.к т.о неподвижна, то  равно скорости частицы, т.е. совпадает с
равно скорости частицы, т.е. совпадает с  , т.е.
, т.е.  . Далее
. Далее  — второй закон Ньютона и
— второй закон Ньютона и  ; Величина
; Величина  —момент силы аксиальный вектор.
—момент силы аксиальный вектор.  ,
,  —плечо силы
—плечо силы 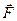 относительно т.О.
относительно т.О.
Т.о производная по  момента импульса
момента импульса  частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы
частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы 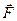 относительно этой точки
относительно этой точки  . Это уравнение называют уравнением моментов.
. Это уравнение называют уравнением моментов.
Если система отсчета является неинерциальной, то в момент силы 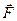 включает в себя как момент сил взаимодействия, так и момент сил инерции (относительно той же т.О). Из уравнения моментов следует что если
включает в себя как момент сил взаимодействия, так и момент сил инерции (относительно той же т.О). Из уравнения моментов следует что если  , то
, то  —равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас
—равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас  , то момент импульса частицы относительно этой точки остается постоянным.
, то момент импульса частицы относительно этой точки остается постоянным.
Уравнение моментов позволяет найти  точки относительно О в любой момент времени если известна
точки относительно О в любой момент времени если известна  частицы относительно точки. Для этого достаточно продифференцировать уравнение
частицы относительно точки. Для этого достаточно продифференцировать уравнение  . Кроме этого, если известна зависимость
. Кроме этого, если известна зависимость  , то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение
, то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение  , тогда
, тогда

Выражение 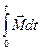 —импульс момента силы подобно
—импульс момента силы подобно  , т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э
, т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э
то время.

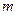 относительно точки О называется вектор
относительно точки О называется вектор  равный
равный  ,
, 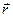 -радиус; -импульс.
-радиус; -импульс. и вектор
и вектор 
 угол между
угол между 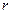 и
и 
 плечо вектора
плечо вектора 
 .
. Т.к т.о неподвижна, то
Т.к т.о неподвижна, то  равно скорости частицы, т.е. совпадает с
равно скорости частицы, т.е. совпадает с  . Далее
. Далее  — второй закон Ньютона и
— второй закон Ньютона и  —момент силы аксиальный вектор.
—момент силы аксиальный вектор.  ,
,  —плечо силы
—плечо силы 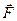 относительно т.О.
относительно т.О. момента импульса
момента импульса  частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы
частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы  . Это уравнение называют уравнением моментов.
. Это уравнение называют уравнением моментов. , то
, то  —равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас
—равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас  , то момент импульса частицы относительно этой точки остается постоянным.
, то момент импульса частицы относительно этой точки остается постоянным. точки относительно О в любой момент времени если известна
точки относительно О в любой момент времени если известна  частицы относительно точки. Для этого достаточно продифференцировать уравнение
частицы относительно точки. Для этого достаточно продифференцировать уравнение  , то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение
, то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение  , тогда
, тогда
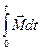 —импульс момента силы подобно
—импульс момента силы подобно  , т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э
, т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э


