Закон Гука при растяжении и сжатии. .
Закон Гука В пределах упругих деформаций деформации прямо пропорциональны нагрузке: F = kΔ l, где F — действующая нагрузка; k — коэффициент. В современной форме:
Получим зависимость σ =Eε, где Е — модуль упругости, характеризует жесткость материала. В пределах упругости нормальные напряжения пропорциональны относительному удлинению. Значение Е для сталей в пределах (2÷ 2, l) • 105 МПа. Планетарными называют передачи, колеса которых движутся подобно планетам солнечной системы: центральные колеса вращаются только вокруг своей оси (называемой центральной), а сателлиты 2, входящие в зацепление с центральными колесами, вращаются вокруг осей центральной и своей. Оси сателлитов закреплены на водиле, вращающемся относительно центральной оси. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:
Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии Используем известные формулы. Закон Гука σ =Eε. Откуда Относительное удлинение В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:
где Δ l — абсолютное удлинение, мм; σ - нормальное напряжение, МПа; / — начальная длина, мм; Е — модуль упругости материала, МПа; N — продольная сила, Н; А — площадь поперечного сечения, мм2; Произведение АЕ называют жесткостью сечения. Ускорение характеризует не только изменение величины скорости, но и изменение ее направления. Очевидно, что быстрота изменения направления вектора скорости, при прочих равных условиях, зависит от степени искривленности траектории. Для количественной оценки этой искривленности вводится понятие кривизны.
|

 ;
;  .
. .
. .
. .
. ;
; 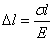 или
или  ,
,


