 Пусть к твердому телу приложена плоская система сил
Пусть к твердому телу приложена плоская система сил  (рис.1.16). Возьмем в теле произвольную точку
(рис.1.16). Возьмем в теле произвольную точку  , которую будем называть центром приведения, и приложим к ней попарно уравновешенные силы
, которую будем называть центром приведения, и приложим к ней попарно уравновешенные силы  и
и 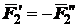 . Заметим, что силы
. Заметим, что силы  и
и  образуют при этом пару сил, так что можно считать силу
образуют при этом пару сил, так что можно считать силу  перенесенной параллельно самой себе в точку
перенесенной параллельно самой себе в точку  - замененной силой
- замененной силой  с присоединением пары
с присоединением пары  . Поступив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил
. Поступив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил  , приложенных в точке
, приложенных в точке  , и совокупности пар
, и совокупности пар  . Сходящиеся силы имеют равнодействующую
. Сходящиеся силы имеют равнодействующую  , приложенную в точке
, приложенную в точке  и равную векторной сумме всех сил системы. Эта сумманазывается главным вектором системы и обозначается
и равную векторной сумме всех сил системы. Эта сумманазывается главным вектором системы и обозначается  .
.
Пары можно заменить одной результирующей парой с моментом  , равным алгебраической суммеих моментов. Так как момент пары равен сумме моментов входящих в нее сил относительно любой точки плоскости пары, то для каждой из складываемых пар
, равным алгебраической суммеих моментов. Так как момент пары равен сумме моментов входящих в нее сил относительно любой точки плоскости пары, то для каждой из складываемых пар
 .
.
Поэтому сумма моментов пар равна сумме моментов самих заданных сил относительно точки  , которая называется главным моментом системы относительно этой точки и обозначается
, которая называется главным моментом системы относительно этой точки и обозначается  . Таким образом, систему сил, произвольно расположенных на плоскости, можно заменить совокупностью одной силы
. Таким образом, систему сил, произвольно расположенных на плоскости, можно заменить совокупностью одной силы  , равной их главному вектору
, равной их главному вектору  , и приложенной в произвольно выбранном центре приведения, и одной пары, момент которой
, и приложенной в произвольно выбранном центре приведения, и одной пары, момент которой  равен главному моменту
равен главному моменту  заданных сил относительно центра приведения. Это утверждение называется теоремой Пуансо о приведении плоской системы сил к данному центру.
заданных сил относительно центра приведения. Это утверждение называется теоремой Пуансо о приведении плоской системы сил к данному центру.
Главный вектор и главный момент системы определяются по формулам:
 ,
,  .
.

 Пусть к твердому телу приложена плоская система сил
Пусть к твердому телу приложена плоская система сил  (рис.1.16). Возьмем в теле произвольную точку
(рис.1.16). Возьмем в теле произвольную точку  , которую будем называть центром приведения, и приложим к ней попарно уравновешенные силы
, которую будем называть центром приведения, и приложим к ней попарно уравновешенные силы  и
и 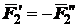 . Заметим, что силы
. Заметим, что силы  и
и  образуют при этом пару сил, так что можно считать силу
образуют при этом пару сил, так что можно считать силу  с присоединением пары
с присоединением пары  . Поступив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил
. Поступив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил  , приложенных в точке
, приложенных в точке  . Сходящиеся силы имеют равнодействующую
. Сходящиеся силы имеют равнодействующую  , приложенную в точке
, приложенную в точке  .
. , равным алгебраической суммеих моментов. Так как момент пары равен сумме моментов входящих в нее сил относительно любой точки плоскости пары, то для каждой из складываемых пар
, равным алгебраической суммеих моментов. Так как момент пары равен сумме моментов входящих в нее сил относительно любой точки плоскости пары, то для каждой из складываемых пар .
. . Таким образом, систему сил, произвольно расположенных на плоскости, можно заменить совокупностью одной силы
. Таким образом, систему сил, произвольно расположенных на плоскости, можно заменить совокупностью одной силы  ,
,  .
.


