Дифференциальные зависимости при изгибе
Первое из двух записанных уравнений дает условие
Из второго уравнения, пренебрегая слагаемым
Рассматривая полученные выражения, совместно можем получить
Полученные соотношения называют дифференциальными зависимостями Д.И. Журавского при изгибе. Анализ дифференциальных зависимостей при изгибе позволяет установить некоторые особенности (правила) построения эпюр изгибающих моментов и поперечных сил: - на участках, где нет распределенной нагрузки q, эпюры Q ограничены прямыми, параллельными базе, а эпюры М - наклонными прямыми; - на участках, где к балке приложена распределенная нагрузка q, эпюры Q ограничены наклонными прямыми, а эпюры М - квадратичными параболами. При этом, если эпюру М строим «на сжатом волокне», то выпуклость параболы будет направлена против направления действия q, а экстремум будет расположен в сечении, где эпюра Q пересекает базовую линию; - в сечениях, где к балке прикладывается сосредоточенная сила, на эпюре ^ Q будут скачки на величину и в направлении данной силы, а на эпюре М - перегибы, острием направленные в направлении действия этой силы; - в сечениях, где к балке прикладывается сосредоточенный момент, на эпюре ^ Q изменений не будет, а на эпюре М - скачок на величину этого момента; - на участках, где Q > 0, момент М возрастает, а на участках, где Q < 0, момент М убывает.
|

 В
В  ыделим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dz. Так как вся балка находится в равновесии, то и элемент dz будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Qy и Mx в общем случае меняются вдоль оси балки, то в сечениях элемента dz будут возникать поперечные силы Qy и Qy+ dQy, а также изгибающие моменты Mx и Mx+dMx.
ыделим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dz. Так как вся балка находится в равновесии, то и элемент dz будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Qy и Mx в общем случае меняются вдоль оси балки, то в сечениях элемента dz будут возникать поперечные силы Qy и Qy+ dQy, а также изгибающие моменты Mx и Mx+dMx.  , следовательно
, следовательно ; (6.5)
; (6.5) , следовательно
, следовательно (6.6)
(6.6) (6.7)
(6.7)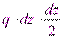 как бесконечно малой величиной второго порядка, найдем
как бесконечно малой величиной второго порядка, найдем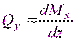 (6.8)
(6.8)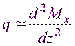 (6.9)
(6.9)


