Решение. 1. Рисуем расчетную схему
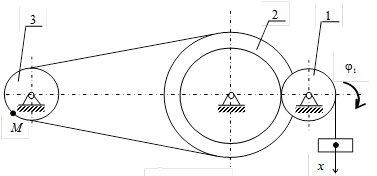
1. Рисуем расчетную схему. Указываем на ней направления скоростей каждого тела.
2. Вычисляем скорость груза 1
В момент времени 3. Вычисляем ускорение груза 1
4. Для определения угловой скорости
Отсюда 5. Запишем уравнение, связывающее угловые скорости колес 2 ω 2 и 3 - ω 3.
Откуда вычисляем- ω 3
или с учетом (5) после подстановки данных
В момент времени t1 Угловое ускорение колеса 3
6. Определим скорость точки М, её центростремительное, вращательное и полное ускорения
Рис.2
Результаты вычислений для заданного момента времени
Скорости и ускорения тела 1 и точки М показаны на рис. 2.
Пример 2 Рассмотрим пример решения задания для механизма, кинематическая схема которого приведена на рис. 3., где ведущим звеном является груз. Задано: закон изменения вертикальной координаты груза x (t) = 30 + 10 t 2, см; радиусы колес R1 = R3 = 10 см, R2 = 30 см, r2 = 20 см. Определить скорость и ускорение точки М для момента времени t1 = 1 c.
Рис.3 Решение Обозначим и покажем на рис.3 точки механизма А, В, D1, D2, через которые передается движение от одного звена (ведущего) к другому (ведомому). Решение задачи начнем с определения скорости груза. Поскольку груз совершает поступательное движение, его можно считать точкой, движение которой задано координатным способом, и движется только вдоль оси x. Проекцию скорости груза на эту ось определим как производную от координаты x по времени
Поскольку знак проекции скорости груза на ось x положительный, вектор скорости направлен вниз, т.е. в положительном направлении оси x.
Рис.4 Скорости всех точек нити, на которой висит груз, одинаковы (нить считается нерастяжимой), скорость точки схода нити с барабана (колеса 1) равна скорости груза. Но точка А схода нити в данный момент времени принадлежит и колесу 1, совершающему вращательное движение вокруг неподвижной оси, что позволяет определить его угловую скорость. Направление угловой скорости колеса 1 соответствует направлению скорости точки А. Запишем теперь алгебраическое значение угловой скорости колеса 1
Колеса 1 и 2 находятся в зацеплении и имеют общую точку В (см. рис.4). Поэтому скорости точек колес, находящихся на их ободьях, одинаковы. При записи алгебраического значения угловой скорости колеса 2 учтем, что внешнее зацепление меняет направление вращения на противоположное
Одинаковы также скорости точек D1 и D2, расположенных на шкивах ременной передачи. Однако здесь направление вращения не изменяется, поэтому
Определим теперь скорость точки M колеса 3 в момент времени t 1 = 1 с. Величина скорости – это произведение модуля угловой скорости на расстояние от точки M до оси вращения, которое равно радиусу
откуда получим полное ускорение точки M
Векторы ускорений показаны на рис. 5. Движение колеса 3 ускоренное, поэтому вращательное ускорение точки M направлено в ту же сторону, что и ее скорость. Центростремительное ускорение всегда направлено к оси вращения. Если в условии будет задан не закон движения груза x(t), а зависимость угла поворота колеса 1 от времени, например, j 1(t) = 3 +t 2, рад, изменения в решении задачи коснутся только начального этапа. Алгебраическое значение угловой скорости колеса 1 определим как производную от его угла поворота по времени Дальнейшее решение задачи не отличается от приведенного примера.
ПРИМЕРЫ РЕШЕНИЯ КОНТРОЛЬНОГО ЗАДАНИЯ К3 Пример 1. Катушка катится без скольжения в вертикальной плоскости по наклонному пути (рис. К3-1).
r = 0.6 м, R = 1 м. Решение Катушка совершает плоскопараллельное движение. Так как качение происходит без скольжения, то скорость точки Р касания катушки с неподвижной поверхностью
где
Определим угловую скорость катушки
Так как скорости точек О и В катушки также пропорциональны их расстояниям до точки Р, то
Направление вращения катушки, а, следовательно, и направления скоростей точек В и О, определяются направлением вектора скорости Пример 2. Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью Найти в положении, указанном на рис. К3-2, угловую скорость стержня, скорости точек В и С, если АВ = 1, 2 м, АС = ВС.
Решение Стержень АВ совершает плоскопараллельное движение. Так как скорости точек А и В направлены параллельно соответствующим направляющим, вдоль которых скользят ползуны, то, восстанавливая из точек А и В перпендикуляры к скоростям этих точек, определим положение мгновенного центра скоростей стержня АВ – точка Р. Треугольник АВР является равнобедренным, следовательно, АВ = ВР = 1, 2м. Скорость точки А пропорциональна расстоянию от этой точки до точки Р: Вычислим угловую скорость стержня АВ
Скорость точки В определим по формуле
Для определения скорости точки С найдем расстояние РС с помощью теоремы косинусов
Тогда скорость точки С
Пример 3. Кривошип ОА длиной r = 1 м вращается с угловой скоростью Определить скорость ползуна В, угловую скорость шатуна
Рис.К3-3 Решение Шатун АВ совершает плоскопараллельное движение. При этом
Найдем положение мгновенного центра скоростей, восстанавливая перпендикуляры к скоростям точек А и В из этих точек. При угле j = 0 (см. рис. К3-3, а) перпендикуляр к скорости
На рис. К3-3, а показано распределение скоростей точек шатуна. При угле поворота кривошипа j = 900 скорости Пример 4. Кривошип ОА = 0, 5м вращается с угловой скоростью w 0А = 10 рад/с и приводит в движение шатун АВ = 4 м. Найти угловую скорость шатуна, скорости точек В и С (АС = 2, 5м), если угол поворота кривошипа j = 450 и ОА ^ АВ (рис.К3-4). Решение Так как кривошип ОА совершает вращательное движение, то
Найдем угловую скорость шатуна АВ
Скорости точек В и С пропорциональны их расстояниям до МЦС:
где ВР =
|

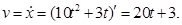
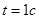 скорость равна
скорость равна 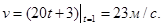
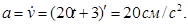
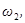 и углового ускорения тела 2 запишем уравнение, связывающее скорость груза v и угловую скорость колеса 2. ω 2 и ω 3. В соответствии со схемой механизма
и углового ускорения тела 2 запишем уравнение, связывающее скорость груза v и угловую скорость колеса 2. ω 2 и ω 3. В соответствии со схемой механизма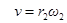
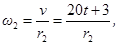
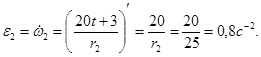
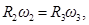
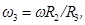


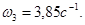
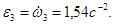

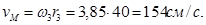
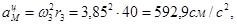
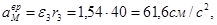
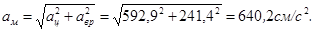
 с приведены в таблице
с приведены в таблице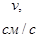
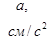
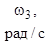

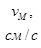
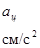
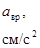

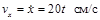 , при t 1 = 1 с vx= 20 см/с.
, при t 1 = 1 с vx= 20 см/с.
 , при t 1 = 1с w1 z= 2рад/с.
, при t 1 = 1с w1 z= 2рад/с. , при t 1 = 1 с w2 z = 1рад/с.
, при t 1 = 1 с w2 z = 1рад/с. , при t 1= 1 с
, при t 1= 1 с 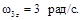
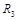 ,
, 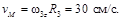 Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис. 4).
Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис. 4).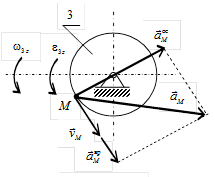 Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости
Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости 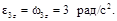 Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным.
Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным. Ускорение точки M определим как геометрическую сумму векторов вращательного и центростремительного ускорений, модули коРис.5 торых вычислим по формулам:
Ускорение точки M определим как геометрическую сумму векторов вращательного и центростремительного ускорений, модули коРис.5 торых вычислим по формулам: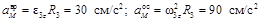 ,
,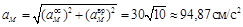 .
.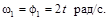
 Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени
Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени  = 2 м/с,
= 2 м/с,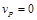 , следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А
, следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А 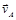 перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС:
перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС: ,
,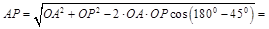
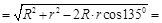 1, 49 м.
1, 49 м.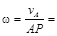 1, 35 рад/с.
1, 35 рад/с. 0, 81 м/с;
0, 81 м/с;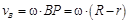 = 0, 54 м/с.
= 0, 54 м/с.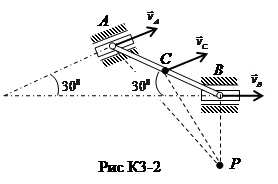
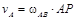 , где
, где  2, 08 м.
2, 08 м.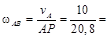 0, 48 рад/с.
0, 48 рад/с.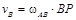 = 0, 48·1, 2 = 0, 58 м/с.
= 0, 48·1, 2 = 0, 58 м/с. 1, 59 м.
1, 59 м.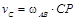 = 0, 76 м/с.
= 0, 76 м/с.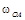 = 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. К3-3.
= 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. К3-3. в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.
в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.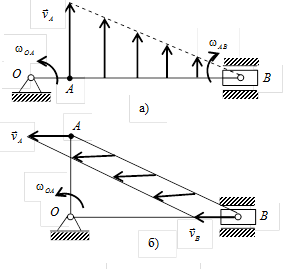
 , так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А
, так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А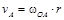 =2·1=2 м/с.
=2·1=2 м/с. пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и
пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и  . Это положение механизма называют «мертвым». Найдем угловую скорость шатуна
. Это положение механизма называют «мертвым». Найдем угловую скорость шатуна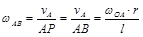 = 0, 5 рад/с.
= 0, 5 рад/с.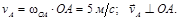
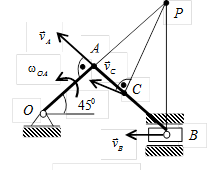 Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.
Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.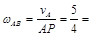 1.25 рад/с.
1.25 рад/с.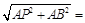
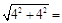 5, 65 м;
5, 65 м;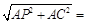
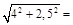 4, 72 м;
4, 72 м;


