Вычисляем искомые величины. Из полученных уравнений определяем SА и SСИз полученных уравнений определяем SА и SС. Для этого подставим в уравнения значения сил и решаем полученную систему линейных уравнений.
Используем метод Крамера. Вычислим определители, из коэффициентов при SВ , SА и значения правых частей уравнений.
Тогда
Ответ: SА =8, 421кН; SB =3, 662кН.
Пример решения задачи из схемы С2 Жестко заделанная у левого конца консольная балка АВ (рис. 6, а) нагружена равномерно распределённой нагрузкой интенсивностью q =5к Н /м, сосредоточенной силой Р =12к Н наклонной к балке под углом a=60° и моментом М =20к Н . м. Определить реакции заделки.
a) б) Рис.6 Решение: 1). Рисуем расчетную схему: ü Объект изучения: рассмотрим равновесие балки АВ. ü Действующие силы: -сосредоточенная сила Р, которую удобно заменить составляющими -равномерно распределённая нагрузка, которую заменим сосредоточенной силой -правый конец балки нагружен моментом m, направленным против хода часовой стрелки. ü Заменяем связи реакциями: Заделку в точке А заменим реакциями связи XA, YA и реактивным моментом mА (рис. 5.2, б). В результате выполненных действий 1-3, расчетная схема принимает вид, указанный на рис.6, б.
|
,
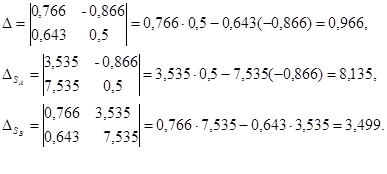
, приложенной посередине,
