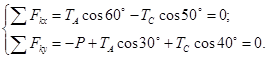Вычисляем искомые величиныИз полученных уравнений определяем SА и SС. Для этого подставим в уравнения значения сил и учтем, что
Решим эту систему относительно SА и SС. При сложении уравнений получим
ОТВЕТ: Цепь АВ растянута, возникающее в не усилие равно SА =15, 532кН. Откос СВ сжат с усилием SВ =21, 96Н.
П Р И М Е Р 2. Электрическая лампа весом 20 Н подвешена к потолку на шнуре АВ и затем оттянута к стене верёвкой ВС (рис.4, а). Определить натяжение: ТА шнура АВ и ТС верёвки ВС, если известно, что угол a =55°, а угол, b =130°. Весом шнура и верёвки пренебречь. Решение: 1). Рисуем расчетную схему: (Углы расставляем согласно значениям, заданным в таблице) ü Выбираем объект изучения (Изучим равновесие узла В, который находится в равновесии при действии двух связей: шнура АВ, верёвки ВС и силы тяжести лампы). ü Расставляем действующие (заданные) силы (Заданной или активной силой является сила тяжести Р, направленная вниз). ü Заменяем действие связей реакциями: (Заменим связи реакциями: шнур АВ реакцией ТА, направленной вдоль шнура к точке подвеса А, а действие верёвки ВС заменим реакцией ТС, также направленной к точке подвеса С).
а) б) Рис.4 2) Введем систему координат и составляем уравнения равновесия (Начало координат выберем в точке В).:
|
. В результате получим следующую систему линейных уравнений.
, следовательно,
; 
.
