Вычисляем искомые величины. Из полученных уравнений определим ТА и ТС
Используем метод Крамера. Вычислим определители, из коэффициентов при ТС, ТА и значения правых частей уравнений.
Тогда
ОТВЕТ: Натяжения шнура и нити равны соответственно
ПРИМЕР 3: Груз G при помощи троса, перекинутого через блок С, поднимается силой Р с постоянной скоростью. Определить усилия в стержнях АС и ВС. Размерами блока и трением на нем пренебрегаем, известно, что угол a=30°, а угол, b=50°, j=45° G=4кН, Р=5кН. Весом стержней пренебречь. Решение: 1). Рисуем расчетную схему: (Углы расставляем согласно значениям, заданным в таблице)
Рис.5 ü Выбираем объект изучения (Изучим равновесие узла С, который находится в равновесии при наличии двух связей: стержня АС и стержня ВС). ü Расставляем действующие (заданные) силы (Заданными или активными силами являются: сила Р и сила тяжести G, направленная вниз). ü Заменяем действие связей реакциями: (Заменим действие стержней АС и ВС реакциями SА и SB, направленными вдоль стержней от узла, считая, что стержни работают на растяжение). 2) Введем систему координат и составляем уравнения равновесия (Начало координат выберем в точке С. Укажем углы между силами и координатными осями)
|
Из полученных уравнений определим ТА и ТС. Для этого решим систему линейных уравнений (здесь 
, 
).
; 
.
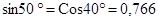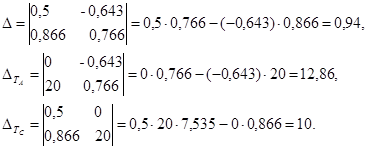
