В поисках новых объяснительных понятий

Невозможность применения в микрофи­зике принципов механистического детерми­низма для объяснения мельчайших явлений была истолкована приверженцами класси­ческой науки как неудача, которую необ­ходимо во что бы то ни стало преодолеть, возвращаясь к традиционной концепции де-

¹ Гейзенберг В. Физика и философия. Гл. 2. С. 21.

терминизма. В этом отношении и Эйнш­тейн примкнул к сторонникам классической науки. Конечно, он глубоко изменил прин­цип описания движения по сравнению с ньютоновской механикой. Тем не менее он сохранил верность классической физике в том, что касается необходимости механи­стического объяснения природных явлений вплоть до мельчайших деталей:

Я мучаюсь, пытаясь вывести из диф­ференциальных уравнений общей теории относительности уравнения движений ма­териальных точек, понимаемых как оди­ночные².

Поиск такого объяснения основывается на уверенности в том, что явления должны быть детерминированы сами по себе и что простая вероятность не может относиться к природе вещей: " Бог не играет в кости" ³, или, иначе, мир может быть устроен лишь в соответствии с правилами абсолютного детерминизма.

Однако до сих пор все попытки сведения наблюдаемых микрофизикой явлений к строгому механистическому детерминиз­му, похоже, оказались неудачными. Эта не­удача соответствует теоретическим обосно­ваниям принципа неопределенности, вы­двинутым сторонниками квантовой теории, в частности Плавком и Гейзенбергом. Дей­ствительно, если верно, что наблюдаемые в микрофизике явления изменяются под воздействием средств наблюдения, то в ре­зультате они принимают случайный харак­тер. Ведь случай, согласно его объективно­му определению, появляется в результате встречи двух независимых причинных ря­дов. Поэтому взаимодействие наблюдае­мых явлений и средств наблюдения в мик­рофизике несет с собой неустранимую до­лю случайности.

Конечно, можно настаивать на том, что сами по себе, независимо от условий на­блюдения, микрофизические явления детер­минированы. В самом деле, утверждение о недетерминированности этих явлений са­мих по себе звучит шокирующе для нашего разума — ведь его основной принцип гла­сит, что " ничего не происходит без основа­ния". Однако требования современной нау-

¹ Einstein A. Lettre ä Born (1926). 'Ibidem.

 

ки существенно экспериментальны. И по­стулировать детерминизм, скрытый за на­блюдаемыми явлениями, не имеет физичес-кого смысла — такой тезис может отно­ситься лишь к формам метафизики, окончательно отвергнутым философией со времен кантовской критики. Так что задача современной философии скорее в том, что­бы изучать новые формы исследования де­терминации в познании природы, дабы из­влечь отсюда новые понятия философии природы и духа.

а) Новый телеологизм

Уже в самой постановке проблем де­терминизма имеется двусмысленность. В самом широком смысле этого термина детерминизм означает требование дете­рминации. Это требование неотделимо от научного мышления вообще. Но оно может требовать только точности в оп­ределении явления и соотнесения его с при­чинами. Поиск исключительно механичес­кой причинности направлен лишь на одну особую форму детерминации — ту, при которой " начальное состояние... однознач­но определяет протекание процесса во все последующее время" ¹. Несомненно, эта форма детерминации не подходит для микрофизики, где из-за соотношения неопределенностей детальное измерение явлений не может избавиться от неточ­ности.

Но в данном случае индетерминация оказывается результатом требования осо­бой формы детерминации, основанной на механической причинности. " Однако и в классической механике уже со времен Лейб­ница известна другая постановка вопроса, которая там также ведет к определенному ответу" ². Согласно механицизму, процесс полностью определен, если " кроме конфи­гурации в один момент времени" известен и " импульс" ³, воздействующий на данную систему в этот момент. Но можно также считать, что система полностью опреде-

¹ Планк М. Единство физической картины мира // Избранные труды. С. 587.

² Там же. 'Там же.

лена, если известны ее конфигурации в два разных момента при условии, что из­вестен и " вариационный принцип" ⁴, объяс­няющий переход от одной конфигурации к другой.

Но еще до Лейбница Ферма и Гюйгенс открыли такой вариационный принцип в области физической оптики. Так, Ферма показал, что " если две точки находятся в различных прозрачных средах, то луч све­та, чтобы пройти от одной точки к другой, преломляется у плоской поверхности, по которой соприкасаются обе среды, таким образом, что употребляет возможно мень­шее количество времени, совершенно так же, как это происходит при отражении от плоской поверхности" ⁵. Надо, однако, за­метить, что соответствующее доказатель­ство предполагает установленным закон отношения синусов. Поэтому более инте­ресным представляется обратное доказа­тельство, в котором Ферма, предполагая известным отношение скоростей в двух прозрачных средах, исходил из принципа, что " свет употребляет при этом прохожде­нии возможно меньшее количество време­ни, чтобы затем вывести из этого постоян­ство отношений синусов" ⁶. Это доказатель­ство показывает, что если даны начальная и конечная точки движения, а также вари­ационный закон этого движения между крайними точками (за возможно короткое время), то промежуточная траектория мо­жет быть полностью определена (согласно закону равенства синусов).

Однако обобщение этого положения бы­ло дано лишь Лейбницем благодаря ис­пользованию исчисления бесконечно ма­лых. Доказательства Ферма и Гюйгенса ос­новывались на определении кратчайшего промежутка времени. Вместо этого чисто количественного определения Лейбниц в качестве предмета исследования взял " наиболее определенное по величине, могу­щее быть как наибольшим, так и наимень­шим в своем порядке" ⁷:

" Там же.

⁵ Гюйгенс X. Трактат о свете. Гл. 3. С. 59—60 (см. там же доказательство Гюйгенса).

'Там же. С. 60.

⁷ Лейбниц Г. В. Анагогический опыт исследо­вания причин // Соч.: В 4 т. М., 1984. Т. 3. С. 132.

 

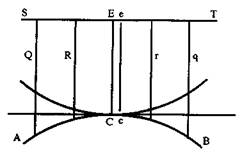
Так, пусть имеется... выпуклая либо вогну­тая кривая AB, а 57" — ось, с которой на кривую опущены ординаты; при этом вид­но, что ординате Q ('или R) соответствует равная ей и являющаяся как бы ее двойни­ком некоторая другая q (или г). Но име­ется особый случай ординаты ЕС, которая оказывается единственной определенной, единственной по своей величине и не име­ет двойника, поскольку две ординаты ЕС и ее сливаются, образуя одну ординату, и эта ордината ЕС оказывается наиболь­шей в случае вогнутой кривой и наимень­шей в случае выпуклой¹.

" Основанием анализа" здесь является един­ственность решения, которое только и дает абсолютную определенность, тогда как лю­бое другое решение выступает как двойст­венное и, следовательно, как недостаточно определенное.

Например, в случае отражения или пре­ломления света, если даны начальная и конечная точка траектории, а также поверх­ность отражения или преломления, то за­дача состоит в определении на этой поверх­ности точки преломления или отражения.

¹ Лейбниц Г. В. Апагогический опыт исследо­вания причин // Соч. Т. 3. С. 132.

При этом оказывается, что принцип Гюй­генса и Ферма (определение через кратчай­шее время) применим не ко всем случаям, так как " в случае вогнутых зеркал оказыва­ется, что путь отраженного луча наидлин­нейший" ², как это видно на рисунке, где у вогнутого зеркала DCD' траектория АС В самая длинная и в то же время более оп­ределенная, чем любая двойственная траек­тория ADB или AD 'В. Таким образом, оп­ределенность обязательно связана не с кра­тчайшим путем, но с " уникальным, единственным, или определенным по своей величине" ³. При отражении решение задачи дается лишь равенством углов падения и отражения, ибо при всяком неравенстве этих углов имеется два симметричных ре­шения или " близнецы" ⁴. Также и в случае преломления решение определяется тем, что оно единственно:

...Преломленный луч, исходящий из точки, находящейся в одной среде, достигает точ­ки, находящейся в другой среде, наиболее определенным, единственным путем, не имеющим, так сказать, пути-близнеца...⁵

Правда, в случае преломления решение та­ково, что время прохождения луча является " в действительности... наиболее кратким" ⁶. Но здесь это лишь следствие, а не принцип доказательства.

Отсюда видно, что принцип, согласно которому природа действует " наикратчай­шими" путями, есть лишь количественное следствие принципа, по которому она дей­ствует " наипростейшими" ⁷ путями. Но " на­ипростейший" означает здесь " наиболее оп­ределенный", а самый определенный — это тот, при котором устраняются другие воз­можные решения, то есть те, возможность которых остается неопределенной. Следо­вательно, принцип, согласно которому при­рода действует простейшими путями

— и который Лейбниц и Мопертюи назва­ли " принципом наименьшего действия",

— может быть выражен в терминах вероят­ности. Действительно, он означает, что из всех возможных решений природа выбира-