Взаимосвязь между уровнем перинательного риска у беременных и частотой послеродовых осложнений
4. Подставляем полученные результаты в формулу:
Вывод: между уровнем риска беременных и частотой послеродовых осложнений выявлен сильная, прямая корреляционная зависимость. Ошибка рангового коэффициента корреляции для нашего случая (? 30) определяется по формуле:
При большом числе наблюдений (n> 30) средняя ошибка рангового коэффициента может быть определена по формуле:
Оценка вероятности коэффициента корреляции проводится по тем же принципам, что используются для другие показателей с расчетом критерия вероятности (t) и учетом числа наблюдений (число степеней свободы вариационных рядов n1=n-2). Полученные результаты сравнивают с табличными значениями. В общем, следует помнить, что оценка вероятности результатов коэффициентов корреляции должна превышать свою ошибку не менее чем в 2, 5 - 3 раза при достаточном числе наблюдений. Для нашего случая mρ =0, 346 и t=ρ / mρ =0, 80/0, 346=2, 31, что, соответственно, ниже граничных значений (t =3, 2 при p< 0, 05). Полученный результат (t) не позволяет сделать вывод о вероятности данного рангового коэффициента корреляции. Целесообразно в данном случае использовать большее число наблюдений. Упрощенный метод оценки рангового коэффициента корреляции предвидит сравнение его с критическими табличными значениями для определенного числа пар наблюдений. Коэффициент вероятности значительней вероятности ошибки не более 5% (p< 0, 05), если пол Для расчета коэффициента прямолинейности корреляции существует много методов. Они определяются целью, характером и объемом исследований, наглядностью вычислительной техники. Один из методов был предложен К, Пирсоном, в научной литературе известный как линейный коэффициент корреляции Пирсона. Формула его расчета:
где: х и у - варианты сравниваемых вариационных рядов; dx и dy - отклонения каждого варианта от своей средней арифметической. Например: определить зависимость между продолжительностью заболевания (годы) и частотой выявления хронических бронхитов в молодом возрасте (до 29 лет).
Таблица 3
Расчет линейного коэффициента корреляции: 1. Определить средние значения для каждого ряда ( 2. Определить отклонения каждого из значений от средней величины dx и dy. 3. Возвести полученные отклонения в квадрат, и рассчитать их суммы: ∑ d2x =42 и ∑ d2y =656. 4. Подставив полученные значения в формулу Пирсона, находим:
Вывод: между продолжительностью курения в молодом возрасте и частотой хронических бронхитов существует сильная прямая связь. Вероятность полученного результата определяется взаимоотношением t=r/mr, где mr при малом числе наблюдений (n< 30) равно:
Для нашего случая коэффициент вероятности:
t=r/ mr =0, 97/0, 1=9, 7. что значительно выше предельно допустимых значений при вероятности ошибки p< 0, 05.
При большом числе наблюдений (n> 30) формула для расчета средней ошибки коэффициента корреляции имеет другой вид:
Прямолинейная корреляционная связь между параметрами характеризуется тем, что каждому из одинаковых измерений одного показателя отвечает определенное среднее значение другого показателя. Данную зависимость можно описать коэффициентом регрессии. Он показывает, на какую величину в среднем изменился другой параметр при изменении первого на определенную единицу измерения. Рассчитывается коэффициент регрессии по формуле:
где
σ x и σ y - средние квадратичные отклонения рядов (х) и (у). Рассмотрим использование коэффициента регрессии на примере. При анализе данных физического развития 7-летних мальчиков получены следующие параметры физического развития за ростом (
Следовательно, при изменении роста на 1 см вес мальчиков в среднем изменится на 0, 28 кг. Определенный коэффициент регрессии можно использовать в уравнении регрессии при прогнозировании ситуации, - какой вес в среднем будет отвечать росту мальчиков 125, 0 см: Yx = Коэффициенты регрессии довольно широко используются для построения уравнений регрессии при разработке многих медико-социальных и клинических проблем, в том числе для оценки физического развития детей и подростков. Данные уравнения представляют собой математическую модель, которая описывает характер взаимосвязи между исследуемыми параметрами. Это особенно актуально при построении много факторных моделей и прогнозировании уровней результативного параметра системы при фиксированных уровнях отдельных компонентов (показателей). Приведенные выше методики расчета парных коэффициентов корреляции являются основой и только первым этапом много факторного корреляционного анализа. Парные коэффициенты показывают характер связи (общего, " неочищенного") между исследуемыми параметрами без учета влияния других факторов. Оценка " чистой" взаимосвязи в много факторных моделях определяется на основании парциальних коэффициентов корреляции. Основанием для их расчета являются парные коэффициенты. Множественный коэффициент корреляции отражает связь одновременно комплекса факторов с исследуемым результативным фактором (клиническими показателями и др.). Еще одним параметром много факторного корреляционного анализа является коэффициент детерминации, который отражает удельный вес (%) влияния факторов, которые изучаются (факторные признаки), на уровень результативных признаков (показатели здоровья населения, клинические показатели и другие). Методики практической реализации много факторного анализа не рассматриваются в данном разделе, потому что они являются достаточно объемными и широко приведены в специальной литературе. Учитывая значительные объемы расчетов, реализация много факторного корреляционного анализа не возможна без использования вычислительной техники. Данные методики реализованы во многих пакетах прикладных программ: SPSS, SТАТІSТІСА, SТАDIА, АХUM, MULTIFAC, STATGRAPHICS рlиs, SAS и других, их полноценное использование в клинических и медико-социальных исследованиях не возможно без знаний основ медицинской статистики. Контрольные вопросы 1. Что такое корреляционная связь, чем она отличается от функциональной? 2. Дайте характеристику формы, направленности и силы связи. 3. Какие методы используют для расчета коэффициента корреляции? 4. Как определяется достоверность коэффициента корреляции? 5. Что такое регрессия?
|

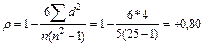
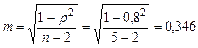
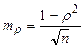
 учтенный результат выше или равен табличному значению. Для нашего примера для 5 пар наблюдений табличное значение ρ =0, 900 (при p< 0, 05), что выше фактического значения. Итак, полученный результат нельзя считать существенным.
учтенный результат выше или равен табличному значению. Для нашего примера для 5 пар наблюдений табличное значение ρ =0, 900 (при p< 0, 05), что выше фактического значения. Итак, полученный результат нельзя считать существенным.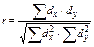
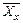 ,
, 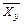 ).
). =0, 97
=0, 97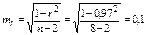
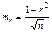

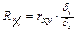
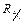 - коэффициент регрессии признаков х по у;
- коэффициент регрессии признаков х по у;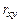 - коэффициент корреляции;
- коэффициент корреляции;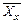 ) и весом (
) и весом (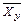 ):
): 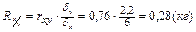
 ) = 26 + 0, 28 (125-120) = 27, 4(кг)
) = 26 + 0, 28 (125-120) = 27, 4(кг)


