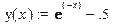Задание 2. 1. Провести уточнение корней методом половинного деления
1. Провести уточнение корней методом половинного деления. В качестве начального приближения выберем 2. Сделать уточнение корней методом простой итерации. Пусть корни отделены и
где функция
где Последнее условие гарантирует сходимость итерационной последовательности
3. Сделать уточнение корней методом хорд или касательных (X, K в таблице 1.1) с заданной точностью Расчетная формула для метода хорд:
для метода касательных:
Значение В результате вычислений по этим формулам может быть получена последовательность приближенных значений корня ПРИМЕРНЫЙ ВАРИАНТ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ НА Maple Отделяем корни графически > y(x): =exp(-x)-0.5;
> plot(y(x), x=-1..3);
Решение с использованием команды solve > solve(y(x), x);
Рассмотрим процедуру, в рамках которой вычисление корней уравнения вида f(x) = 0 осуществляется методом половинного деления интервала. Ниже приведен код процедуры DoublDiv), согласно которой находятся корни выражения ff. Переменная, относительно которой ищутся корни, а также интервал определяются равенством xint. Погрешность задается параметром epsilon. > DoublDiv: =proc(ff, xint, epsilon) > local x, a, b, c, f, i; > x: =lhs(xint); > a: =op(rhs(xint))[1]; > b: =op(rhs(xint))[2]; > f: =unapply(evalf(ff), x); > if f(a)*f(b)> 0 then print(" Неверное введенный интервал"); > else if f(a)*f(b)< 0 then > while (abs(b-a)> epsilon and f(c)< > 0) > do > c: =(a+b)/2; > if f(a)*f(c)> 0 then a: =c; > else b: =c; > end if; > end do; > else > if f(a)=0 then c: =a; > else c: =b; > end if; > end if; > x=evalf(c); > end if; > end proc: Основная часть кода данной процедуры нужна для отслеживания особых ситуаций, когда в процессе поиска решения на одном из этапов пробная точка случайно совпадает с корнем. Однако прежде выполняется ряд инициализаций. Так, локальная переменная х определяется как левая часть равенства xint, указанного параметром процедуры. Переменным а и b присваиваются в качестве значений левая и правая границы диапазона, на котором ищется корень. А переменная f определяется как функциональная зависимость, соответствующая выражению, для которого ищутся корни. Ниже приведены результаты использования разработанной процедуры для выражения. > F: =exp(-t)-0.5;
> DoublDiv(F, t=0..3, 0.000001);
Процедура для вычисления корней уравнения методом секущих может быть получена из процедуры вычисления корней методом половинного деления, если заменить оператор присваивания значения переменной с и условие проверки точности. В качестве верхней границы для точности результата может быть выбран модуль отношения значения функции в точке предполагаемого решения (в процедуре — это f (с)) и минимального значения для производной этой функции на рассматриваемом интервале (параметр М). Вот код для этой процедуры. > khorda: =proc(ff, xint, epsilon, M) > local x, a, b, c, f, i; > x: =lhs(xint); > a: =op(rhs(xint))[1]; > b: =op(rhs(xint))[2]; > f: =unapply(evalf(ff), x); c: =b-f(b)*(b-a)/(f(b)-f(a)); > if f(a)*f(b)> 0 then print(" Неверное введенный интервал"); > else if f(a)*f(b)< 0 then > while (abs(f(c)/M)> epsilon and f(c)< > 0) > do > if f(a)*f(c)> 0 then a: =c; > else b: =c; > end if; c: =b-f(b)*(b-a)/(f(b)-f(a)); > end do; > else > if f(a)=0 then c: =a; > else c: =b; > end if; > end if; > x=evalf(c); > end if; > end proc: > F1: =exp(-t)-0.5;
Теперь воспользуемся процедурой khorda(), предварительно оценив, что производная для Fl(x) по абсолютной величине меньше ехр(-3) на рассматриваемом интервале быть не может. Эту величину, преобразованную в формат числа с плавающей точкой, и указываем последним параметром процедуры khorda(). > khorda(F1, t=0..3, 0.000001, evalf(exp(-3)));
Как видим, результаты в пределах погрешности полностью совпадают.
|

 , затем исследуем функцию на концах отрезков
, затем исследуем функцию на концах отрезков 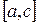 и
и  . Выбирается тот отрезок, у которого значение функции на концах имеет противоположные знаки. Процесс продолжается до тех пор, пока не выполнится условие
. Выбирается тот отрезок, у которого значение функции на концах имеет противоположные знаки. Процесс продолжается до тех пор, пока не выполнится условие  . Точность
. Точность  принять равной
принять равной 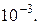
 содержит единственный корень. Уравнение (1.1) приведем к итерационному виду:
содержит единственный корень. Уравнение (1.1) приведем к итерационному виду: (1.2)
(1.2)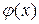 дифференцируема на
дифференцируема на 
 . Функцию
. Функцию  (1.3)
(1.3) находится из условия
находится из условия  , для
, для  .
. к корню
к корню  . Условием окончания счета будем считать выполнение неравенства
. Условием окончания счета будем считать выполнение неравенства
 (1.4)
(1.4) .
.
 ,
, ,
,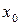 для метода хорд и начальная точка для метода касательных выбирается из условия выполнения неравенства
для метода хорд и начальная точка для метода касательных выбирается из условия выполнения неравенства  .
. . Процесс вычислений заканчивается при выполнении условия
. Процесс вычислений заканчивается при выполнении условия  <
<  (
( ). В каждом случае вывести на печать количество итераций, необходимых для достижения заданной точности.
). В каждом случае вывести на печать количество итераций, необходимых для достижения заданной точности.