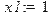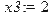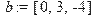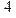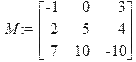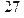Задание 3. Решить систему (2.1) методом Зейделя

Решить систему (2.1) методом Зейделя.

Метод Зейделя отличается от метода простой итерации тем, что найдя какое-то значение для компоненты, мы на следующем шаге используем его для отыскания следующей компоненты. Вычисления ведутся по формуле

(2.8)

Каждое из условий (2.4)-(2.6) является достаточным для сходимости итерационного процесса по методу Зейделя. Практически же удобнее следующее преобразование системы (2.2). Домножая обе части (2.2) на А^Т, получим эквивалентную ей систему

,

где = и d = . Далее, поделив каждое уравнение на , приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса. Очевидно, схема метода Зейделя позволяет в ряде случаев находить решение за меньшее число итераций, чем в методе простой итерации.

 

ПРИМЕРНЫЙ ВАРИАНТ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ НА MAPLE

Пример. Решить систему уравнений

x1+2*x2+3*x3=7,

x1-3*x2+2*x3=5,

x1+x2+x3=3.

Решение системы используя команду solve.

> restart;

> solve({x1+2*x2+3*x3=7, x1-3*x2+2*x3=5, x1+x2+x3=3}, [x1, x2, x3]);

Решение линейной системы уравнений Ax=b.

Используя команду linsolve(A, b).

> restart;

> with(linalg):

> A: = matrix(3, 3, [1, 2, 3, 1, -3, 2, 1, 1, 1]);

> b: = vector([7, 5, 3]);

> linsolve(A, b);

Решение линейной системы методом Гаусса

> restart;

> with(linalg):

> A: = matrix(3, 4, [1, 2, 3, 7, 1, -3, 2, 5, 1, 1, 1, 3]);

> gausselim(A, 'r', 'd');

Из третей строчки получаем, что x3=2, подставляем во второе полученное x3 и находим x2=0, аналогично подставляя в первое равенство, получаем x1=1.

Вычисление решения системы по формуле x=C*b

C - матрица обратная к матрице A

> restart;

> with(linalg):

> A: = matrix(3, 3, [1, 2, 3, 1, -3, 2, 1, 1, 1]);

> C: =inverse(A);

> b: = vector([7, 5, 3]);

> multiply(C, b);

Решение системы методом Крамера

> restart;

> with(linalg):

> B: =matrix(3, 3, [1, 2, 3, 1, -3, 2, 1, 1, 1]);

> det(B);

> B1: =matrix(3, 3, [7, 2, 3, 5, -3, 2, 3, 1, 1]);

> det(B1);

> B2: =matrix(3, 3, [1, 7, 3, 1, 5, 2, 1, 3, 1]);

> det(B2);

> B3: =matrix(3, 3, [1, 2, 7, 1, -3, 5, 1, 1, 3]);

> det(B3);

> x1: =det(B1)/det(B); x2: =det(B2)/det(B); x3: =det(B3)/det(B);

 

> #Вычисление норм вектора и матрицы

> with(linalg):

> b: = vector([0, 3, -4]);

> norm(b);

> M: =matrix(3, 3, [-1, 0, 3, 2, 5, 4, 7, 10, -10]);

> norm(M);

>

Таблица 2.1

 

№ вар.
	0.35 0.12 - 0.13	0.12 0.71 0.15	- 0.13 0.15 0.63	0.10 0.26 0.38
	0.71 0.10 - 0.10	0.10 0.34 0.64	0.12 - 0.04 0.56	0.29 0.32 - 0.10
	0.34 - 0.04 0.06	- 0.04 0.44 0.56	0.10 - 0.12 0.39	0.33 - 0.05 0.28
	0.10 - 0.04 - 0.43	- 0.04 0.34 0.05	- 0.63 0.05 0.13	- 0.15 0.31 0.37
	0.63 0.05 0.15	0.05 0.34 0.10	0.15 0.10 0.71	0.34 0.32 0.42
	1.20 - 0.50 - 0.30	- 0.20 1.70 0.10	0.30 - 1.60 - 1.50	- 0.60 0.30 0.40
	0.30 - 0.10 - 1.50	1.20 - 0.20 - 0.30	- 0.20 1.60 0.10	- 0.60 0.30 0.70
	0.20 0.58 0.05	0.44 - 0.29 0.34	0.91 0.05 0.10	0.74 0.02 0.32
	6.36 7.42 1.77	1.75 19.03 0.42	1.0 1.75 6.36	41.70 49.49 27.67
	3.11 - 1.65 0.60	- 1.66 3.15 0.78	- 0.60 - 0.78 - 2.97	- 0.92 2.57 1.65
	1.20 - 0.20 - 0.30	- 0.20 1.60 - 0.10	0.30 - 0.10 1.50	- 0.60 0.30 - 0.40
	- 3 0.5 0.5	0.5 - 6 0.5	0.5 0.5 - 3	- 56.5 - 100 - 210
	3.5	- 1	- 1 4.5	0.6 - 0.7 2.6
	0.20 0.58 0.05	0.44 -0.29 0.34	0.05 0.81 0.20	0.74 0.02 0.32

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. К какому типу - прямому или итерационному - относится метод Гаусса?

2. В чем заключается прямой и обратный ход в схеме единственного деления?

3. Как организуется, контроль над вычислениями в прямом и обратном ходе?

4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений?

5. Как формулируется достаточные условия сходимости итерационного процесса?

6. Как эти условия связаны с выбором метрики пространства?

7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?

 

Лабораторная работа №3