Уплотнить часть таблицы заданной на отрезке  функции, используя интерполяционный многочлен Ньютона (3.5), ограничиваясь тремя первыми членами формулы и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке
функции, используя интерполяционный многочлен Ньютона (3.5), ограничиваясь тремя первыми членами формулы и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке  с шагом
с шагом  . Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.
. Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.
 , (3.5)
, (3.5)
где  .
.
 , (3.6)
, (3.6)
Формула (3.5) называется первой интерполяционной формулой Ньютона. Если вычисляемое значение переменной ближе к концу отрезка  , то применяют вторую формулу Ньютона – интерполирование назад (формула (3.7)).
, то применяют вторую формулу Ньютона – интерполирование назад (формула (3.7)).
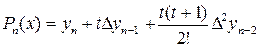 (3.7)
(3.7)
где  и
и  .
.
Таблица 3.7
Таблица 3.8
| №
| 
| 
| 
| 
| № таблицы
|
|
| 0.65
| 0.80
| 0.05
| 0.01
| 3.6
|
|
| 0.25
| 0.40
| 0.05
| 0.025
| 3.5
|
|
| 0.75
| 0.90
| 0.05
| 0.01
| 3.6
|
|
| 0.70
| 0.85
| 0.05
| 0.025
| 3.6
|
|
| 0.80
| 0.95
| 0.05
| 0.025
| 3.6
|
|
| 0.1
| 0.25
| 0.05
| 0.025
| 3.5
|
|
| 0.15
| 0.3
| 0.05
| 0.025
| 3.5
|
|
| 0.7
| 0.85
| 0.05
| 0.025
| 3.6
|
|
| 0.2
| 0.35
| 0.05
| 0.01
| 3.5
|
|
| 0.80
| 0.95
| 0.05
| 0.01
| 3.6
|
|
| 0.2
| 0.35
| 0.05
| 0.01
| 3.5
|
|
| 0.75
| 0.90
| 0.05
| 0.01
| 3.6
|
|
| 0.65
| 0.80
| 0.05
| 0.01
| 3.6
|
|
| 0.20
| 0.35
| 0.05
| 0.025
| 3.5
|
|
| 0.25
| 0.4
| 0.05
| 0.01
| 3.5
|
Примерный фрагмент выполнения работы НА MAPLE.
> x0: =-1; x1: =0; x2: =1; y0: =-12; y1: =0; y2: =0;





> L(x): =(y0*(x-x1)*(x-x2))/((x0-x1)*(x0-x2))+(y1*(x-x0)*(x-x2))/((x1-x0)*(x1-x2))+(y2*(x-x0)*(x-x1))/((x2-x0)*(x2-x1));

> plot(L(x), x=-1..3);


 функции, используя интерполяционный многочлен Ньютона (3.5), ограничиваясь тремя первыми членами формулы и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке
функции, используя интерполяционный многочлен Ньютона (3.5), ограничиваясь тремя первыми членами формулы и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке  . Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.
. Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6. , (3.5)
, (3.5) .
. , (3.6)
, (3.6) , то применяют вторую формулу Ньютона – интерполирование назад (формула (3.7)).
, то применяют вторую формулу Ньютона – интерполирование назад (формула (3.7)).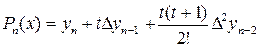 (3.7)
(3.7) и
и  .
.




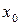
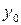
 =
= 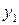 -
- 


 =
= 



 =
=