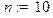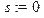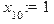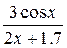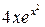Примерный фрагмент выполнения лабораторной работы на Maple. Вычислить интеграл от заданной функции на отрезке [a,b] по формуле трапеций и прямым способом
Вычислить интеграл от заданной функции на отрезке [a, b] по формуле трапеций и прямым способом. 1. Метод трапеций. > restart; > x: =array(0..10);
> a: =0; b: =1; n: =10; h: =(b-a)/n;
> x[0]: =a; s: =0;
> for i from 1 to 9 do x[i]: =x[0]+h*i; s: =s+h*(0.37*sin(x[i])): end do: > evalf(%);
> x[10]: =x[0]+10*h;
> s: =s+h*(0.37*sin(x[0])+0.37*sin(x[10]))/2: > evalf(%);
2. Прямой способ. > Int(0.37*sin(x), x=0..1);
Если хочется представить его в виде десятичной дроби (с некоторой точностью) воспользуйтесь функцией evalf. > evalf(%);
Символ % обозначается последнее вычисленное Maple выражение, %% – предпоследнее, %%% — предпредпоследнее (а вот обозначения %%%% уже не существует). Таблица 4.1
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Каковы преимущества формулы парабол по сравнению с формулой трапеций и следствием чего являются эти преимущества? 2. Верны ли формулы (4.2), (4.4) для неравноотстоящих узлов? 3. В каких случаях приближенные формулы трапеций и парабол оказываются точными? 4. Как влияет на точность численного интегрирования величина шага? 5. Каким способом можно прогнозировать примерную величину шага для достижения заданной точности интегрирования? 6. Можно ли добиться неограниченного уменьшения погрешности интегрирования путем последовательного уменьшения шага?
|