Примерный фрагмент выполнения лабораторной работы
> restart; > with(linalg): Warning, the protected names norm and trace have been redefined and unprotected > x: =array(1..4): y: =array(1..4): > x[1]: =0: y[1]: =0.5: x[2]: =1: y[2]: =2: x[3]: =2: y[3]: =4: x[4]: =3: y[4]: =8: > mx2: =0: mx: =0: mxy: =0: my: =0: > for i from 1 to 4 do mx2: =mx2+x[i]*x[i]/4; end do: > evalf(%);
> for i from 1 to 4 do mx: =mx+x[i]/4; end do: > evalf(%);
> for i from 1 to 4 do mxy: =mxy+x[i]*y[i]/4; end do: > evalf(%);
> for i from 1 to 4 do my: =my+y[i]/4; end do: > evalf(%);
> mx2*a+mx*b=mxy; mx*a+b=my;
> solve({mx2*a+mx*b=mxy, mx*a+b=my}, {a, b});
> Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов: > with(CurveFitting): > LeastSquares([[0, 0.5], [1, 2], [2, 4], [3, 8]], x);
> LeastSquares([[0, 0.5], [1, 2], [2, 4], [3, 8]], x, curve=a*x^2+b*x+c);
>
Таблица 6.1
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. В чем суть приближения таблично заданной функции по методу наименьших квадратов? 2. Чем отличается этот метод от метода интерполяции? 3. Каким образом сводится задача построения приближающих функций в виде различных элементарных функций к случаю линейной функции? 4. Может ли сумма квадратов уклонений для каких-либо приближающих функций быть равной нулю? 5. Какие элементарные функции используются в качестве приближающих функций? 6. Как найти параметры для линейной и квадратичной зависимости, используя метод наименьших квадратов?
|



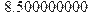





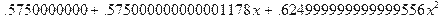

 №
№





