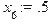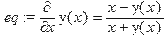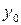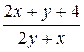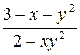Примерный фрагмент выполнения лабораторной работы на Maple

Решить дифференциальное уравнение y’=f(x, y) методом Эйлера на отрезке [a, b] с шагом h c начальным условием y(a)=y₀ , f(x, y)=(x-y)/(x+y), a=0, b=1, h=0.1, y₀=1.

 

> x: =array(0..10): y: =array(0..10):

> x[0]: =0: y[0]: =1: h: =0.1:

> for i from 0 to 9 do x[i+1]: =x[0]+h*i; y[i+1]: =y[i]+h*(x[i]-y[i])/(x[i]+y[i]); end do;

Команда решения дифференциального уравнения будет иметь вид dsolve(eq, vars, type=numeric, options), где eq – уравнения, vars – список неизвестных функций, options – параметры, позволяющие указать метод численного интегрирования дифференциального уравнения. В Maple реализованы такие методы: method=rkf45 - метод Рунге-Кутта-Фельберга 4-5-ого порядка (установлен по умолчанию); method=dverk78 – метод Рунге-Кутта 7-8 порядка; mtthod=classical – классический метод Рунге-Кутта 3-его порядка; method=gear и method=mgear – одношаговый и многошаговый методы Гира.

График численного решения дифференциального уравнения можно построить с помощью команды odeplot(dd, [x, y(x)], x=x1..x2), где в качестве функции используется команда dd: =dsolve({eq, cond}, y(x), numeric) численного решения, после нее в квадратных скобках указывают переменную и неизвестную функцию [x, y(x)], и интервал x=x1..x2 для построения графика.

> restart;

> eq: =diff(y(x), x)=(x-y(x))/(x+y(x));

> de: =dsolve({eq, y(0)=1}, y(x), numeric);

> de(0.9);

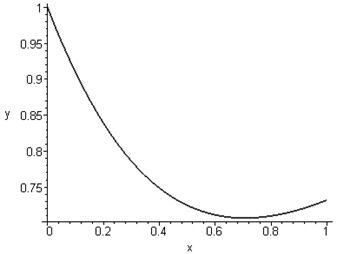
> with(plots):

Warning, the name changecoords has been redefined

> odeplot(de, [x, y(x)], 0..1, thickness=2);

>

Таблица 5.1

N	Функция
					0.1
					0.1
					0.1
					0.1
					0.1
					0.1
					0.1
					0.1
					0.1
					0.1
		1.5	2.5	2.2	0.1
					0.1
		0.1	1.1	1.25	0.1
					0.1
				1.7	0.1

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Проверить для дифференциального уравнения условия теоремы существования и единственности.

2. На какие основные группы подразделяются приближенные методы решения дифференциальных уравнений?

3. В какой форме можно получить решение дифференциального уравнения по методу Эйлера?

4. Каков геометрический смысл решения дифференциального уравнения методом Эйлера?

5. В какой форме можно получить решение дифференциального уравнения по методу Рунге-Кутта?

6. Какой способ оценки точности используется при приближенном интегрировании дифференциальных уравнений методами Эйлера и Рунге-Кутта?

7. Как вычислить погрешность по заданной формуле, используя метод двойного пересчета?