Тема: Численное интегрированиеФормулы, используемые для приближенного вычисления однократных интегралов, называют квадратурными формулами. Простой прием построения квадратурных формул состоит в том, что подынтегральная функция
Предполагается, что отрезок При определенных допущениях получаем из (4.1) формулу трапеций
где Имеем следующую оценку погрешности метода интегрирования по формуле трапеций (4.2):
Во многих случаях более точной оказывается формула Симпсона (формула парабол):
Для формулы Симпсона имеем следующую оценку погрешности:
|
заменяется на отрезке 
интерполяционным многочленом, например, многочленом Лагранжа 
; для интеграла имеем приближенное равенство
» 
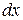(4.1)
разбит на 
частей точками (узлами)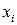 
, наличие которых подразумевается при построении многочлена 
(4.2)
- значения функции в узлах интерполяции.
где 
, 
. (4.3)
(4.4)
где 
, 
.
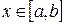