Тема: Численное решение уравнений в частных производных
Рассмотрим смешанную задачу для уравнения теплопроводности, а именно, найти функцию
начальному условию
и краевым условиям
Задачу будем решать методом сеток (конечных разностей). В основе метода лежит идея замены производных конечно-разностными отношениями. Ограничимся случаем двух независимых переменных. Пусть в плоскости хОу имеется некоторая область
Рис 1 Построим на плоскости два семейства параллельных прямых:
Точки пересечения этих прямых назовем узлами. Два узла называются соседними, если они удалены друг от друга в направлении оси Ох или Оу на расстояние, равное шагу сетки h или l соответственно. Выделим узлы, принадлежащие области G+Г, а также некоторые узлы, не принадлежащие этой области, но расположенные на расстоянии, меньшем чем шаг, от границы Г. Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними (узел А, рис. 1). Оставшиеся из выделенных узлов называются граничными (узлы В, С). Обозначим Значения искомой функции и=и(х, у) в узлах сетки будем обозначать через
В граничных точках воспользуемся формулами вида
Аналогично заменяются частные производные второго порядка
Сделаем переход от уравнения вида
После замены
При
Пусть
где
|

 , удовлетворяющую уравнению
, удовлетворяющую уравнению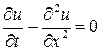 (7.1)
(7.1) , (7.2)
, (7.2) ,
,  . (7.3)
. (7.3) с границей
с границей  (рис. 1).
(рис. 1).
 ,
,  , i=0, 1, 2, …, k=0, 1, 2, …
, i=0, 1, 2, …, k=0, 1, 2, …
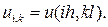 В каждом внутреннем узле
В каждом внутреннем узле  заменим частные производные разностными отношениями:
заменим частные производные разностными отношениями:

 ,
,  .
.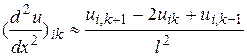
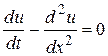 к разностному уравнению
к разностному уравнению -
-  =0.
=0. и преобразований получаем уравнение для вычисления внутренних узлов
и преобразований получаем уравнение для вычисления внутренних узлов (7.4)
(7.4)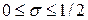 разностное уравнение (7.4) устойчиво [7]. Наиболее простой вид уравнение имеет при
разностное уравнение (7.4) устойчиво [7]. Наиболее простой вид уравнение имеет при  В этом случае уравнение (7.2) запишется в виде
В этом случае уравнение (7.2) запишется в виде (7.5)
(7.5) (x, t) – точное решение задачи (7.1)-(7.3),
(x, t) – точное решение задачи (7.1)-(7.3),  – отклонение точного значения от вычисленного по методу сеток. Тогда погрешность вычислений может быть вычислена по формуле
– отклонение точного значения от вычисленного по методу сеток. Тогда погрешность вычислений может быть вычислена по формуле , (7.6)
, (7.6) =
=  , где
, где 



