ВЫЧИСЛЕНИЯ И ОПЕРАЦИИ В MAPLE
Приведем примеры решения некоторых типовых математических задач. Пример 1. Вычислить: Решение. На экране набираем с клавиатуры > x: =1.5; y: =-1.6; { после; нажимаем на Enter и получаем следующий результат}
> 10*x*x-5*y*y; {нажимаем на Enter}
Пример 2. Преобразовать в стационарный вид многочлен:
Решение. На экране набираем исходное выражение > res: =(a+2*b)*(a-2*b)*(a*a+4*b*b);
> collect(res, {a, b}, distributed);
Пример3. Решить уравнение: Решение. Вводим уравнение > f: =2*(5*x-1)^2+35*x-11;
> solve(f, x); {Важно подчеркнуть тот момент, что Maple находит все решения в том числе и комплексные корни}
Пример 4. Решить систему уравнений:
Решение. Набираем команду solve и систему уравнений > solve({x^2+y+8=x*y, y-2*x=0}, {x, y});
Пример 5. Решить неравенство: Решение. На экране после знака > набираем слово solve затем в скобках наше неравенство > solve(5*x - 3 < 4, x);
Пример 6. Построить график функции y=2*sin(2*x). Решение. Для построения графиков используем команду plot, в скобках указываем функцию, и промежуток, на котором определена абсцисса > plot(2*sin(2*x), x=-5..5);
Пример 7. Построить графики функций:
Решение. Решение аналогично предыдущему примеру. Для построения двух графиков одновременно в одной системе координат вводим их через запятую. > y(x): =4*sin(2*x+3); g(x): =x*x-4*x+3;
> plot({y(x), g(x)}, x=0..4);
Пример 8. Построить график функции z=sin(x*x+y*y) для x от -2 до 2 и y от -2 до 2. Фрагмент выполнения задания приведен ниже. Решение. > plot3d(sin(x*x+y*y), x=-2..2, y=-2..2);
Пример 9. Вычислить предел многочлена: Решение. Выражение > limit(2*x^3-3*x*x+3, x=2);
Пример 10. Вычислить производную: Решение. > diff(cos(x)+x*sin(x), x);
Пример 11. Вычислить неопределенный интеграл: Решение. > int(x^2+cos(x), x);
Пример 12. Вычислить определенный интеграл: Решение. > int((x*x+1)^(1/2), x=0..1);
Пример 13. Вычислить максимум и минимум функции Решение. > restart; > maximize(x*exp(-x), x=0..2);
> evalf(%);
> minimize(x*exp(-x), x=0..2);
Пример 14. Даны матрицы А и В. Найти Решение. > restart; > with(linalg): > A: =matrix([[1, 0], [0, -1]]); > B: =matrix([[-5, 1], [7, 4]]);
> multiply(A, B);
> evalm(A+B);
> inverse(B);
Проверка: > multiply(B, %);
> transpose(B);
|

 при x=1, 5 и y=-1, 6.
при x=1, 5 и y=-1, 6.


 .
.

 .
.



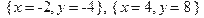
 .
.

 и
и

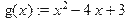


 при
при  .
. при
при  в среде Maple пишем следующим образом
в среде Maple пишем следующим образом
 .
.
 .
.
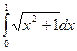 .
.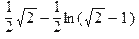
 на отрезке [0, 2].
на отрезке [0, 2].


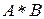 ,
,  ,
, 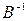 ,
,  .
.









