Tема: Решение уравнения c одной переменной
Рассмотрим уравнение
где Всякое значение Найти корни уравнения вида (1.1) точно удается лишь в редких случаях. Кроме того, часто уравнение содержит коэффициенты, известные лишь приблизительно и следовательно, сама задача о точном определении корней уравнения теряет смысл. Разработаны методы численного решения уравнений вида (1.1), позволяющие отыскать приближенные значения корней этого уравнения. При этом приходится решать две задачи: 1) отделение корней, т. е. отыскание достаточно малых областей, в каждой из которых заключен только один корень уравнения; 2) вычисление корней с заданной точностью. Воспользуемся известным результатом математического анализа: если непрерывная функция принимает на концах некоторого интервала значения разных знаков, то интервал содержит по крайней мере один корень уравнения. Для выделения областей, содержащих один корень, можно использовать, например, графический способом, либо двигаясь вдоль области определения с некоторым шагом, проверять на концах интервалов условие смены знака функции. Для решения второй задачи существует многочисленные методы, из которых рассмотрим четыре: метод итераций, метод половинного деления, метод хорд, метод касательных.
|
(1.1)
определена и непрерывна на некотором конечном или бесконечном интервале 
.
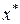, обращающее функцию 
в нуль,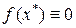 
, называется корнем уравнения (1.1), а способ нахождения этого значения 
