Проверка гипотезы о нормальности для переменной Эффективность

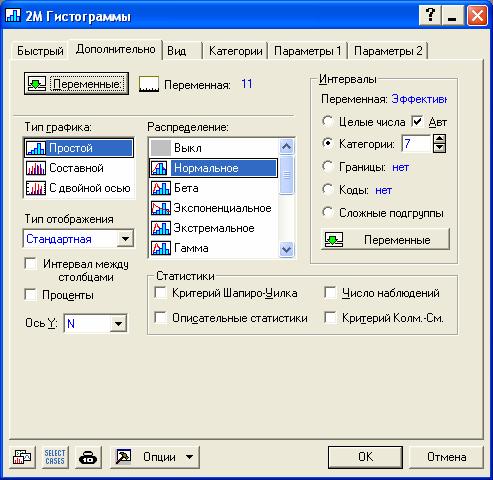
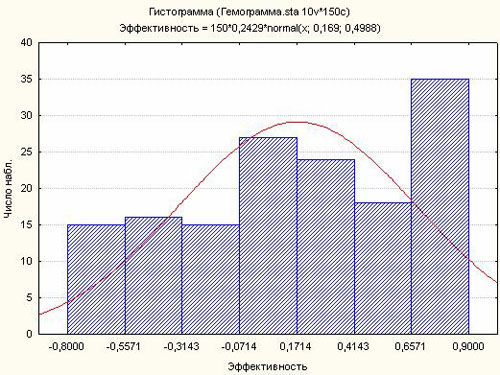
Для ответа на поставленные вопросы можно использовать T-критерий переменной Эффективность. Этот критерий требует нормальность распределения переменной, поэтому перед использованием проверим гипотезу о нормальности.

Сначала проверим визуальными методами.

Построим гистограмму по переменной Эффективность. Для этого выберем из меню пункт Графика / Гистограммы.

На вкладке Дополнительно укажем: Распределение = Нормальное, количество категорий – 7 (приблизительное значение двоичного логарифма от 150, то есть от количества наблюдений), выберем переменную – Эффективность.

 

 

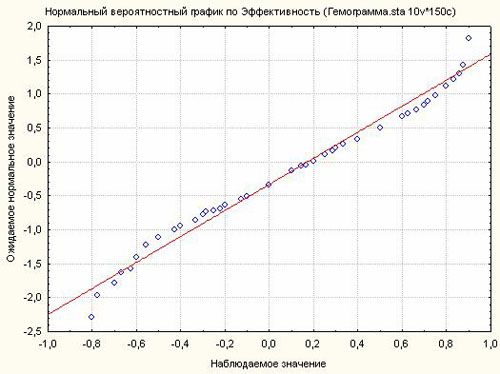
Гипотеза о нормальности кажется очень неправдоподобной (особенно «плохо» выглядят крайние столбцы).

Тот же вывод следует сделать по нормальному вероятностному графику.

 

 

Если наблюдаемые значения (откладываемые по оси X) были бы распределены нормально, то все значения на графике должны были попасть на прямую линию. Однако этого не наблюдается.

 

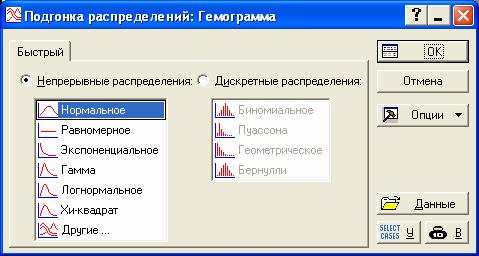
Теперь вычислим некоторые описательным статистики для переменной Эффективность.

На вкладке Дополнительно диалога Описательные статистики поставим галочки в полях Асимметрия, стандартная ошибка асимметрии, Эксцесс, Стандартная ошибка эксцесса. Нажмём OK.

Судя по значению Асимметрии, распределение переменной Эффективность можно считать нормальным (0 «почти что» содержится в интервале Ассиметрия ± Стандартная ошибка Асимметрии).

Но судя по значению Эксцесса, гипотезу о нормальности следует отклонить. Как правило, если найдена хотя бы одна существенная «нестыковка», гипотезу смело отклоняют, в то время как соответствие даже всем известным критериям ещё не влечёт справедливость гипотезы.

В заключении обратимся к модулю Подгонка распределения.

 

 

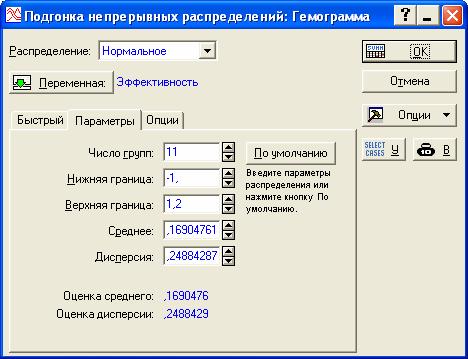
Выберем пункт Нормальное в левом столбце, нажмём OK. В появившемся окне укажем в качестве переменную (Эффективность).

 

 

Нажмём OK.

Обратите внимание: значение p = 0, 00031, то есть значительно меньше 5%. Это значит, что гипотезу о нормальности следует отклонить.

Итак, окончательный вывод: Распределение переменной Эффективность существенно отличается от нормального распределения.