Теоретическое введение. Рассмотрим колеблющуюся механическую систему, положение которой может быть задано с помощью одной переменной
РАБОТА № 1
Рассмотрим колеблющуюся механическую систему, положение которой может быть задано с помощью одной переменной, которую мы обозначим через «х». В этом случае потенциальная энергия системы будет функцией этой переменной, т.е. Разложим функцию
Ограничиваясь малыми колебаниями, будем пренебрегать высшими степенями «х». Тогда учитывая, что
Коэффициент По определению, сила, действующая на систему,
Силы, определяемые по этой формуле, независимо от их природы, получили название квазиупругих сил. Система, движущаяся под действием квазиупругой силы, называется одномерным гармоническим осциллятором. По второму закону Ньютона, для одномерного гармонического осциллятора можно получить
Это выражение можно преобразовать к виду
где Мы получили уравнение движения одномерного гармонического осциллятора. Его решение Примером системы, совершающей гармонические колебания, является тело подвешенное на длинной нити (маятник). Период колебаний маятника определяется по приближенной формуле, пригодной только для малых амплитуд:
где I - момент инерции маятника относительно оси колебаний, m - масса маятника,
g - ускорение свободного падения. В настоящей работе проводится проверка соотношения 1.1 в случае, когда маятник можно приближенно считать математическим, т.к. масса маятника сосредоточена в области, размеры которой малы по сравнению с длиной маятника. Исследуемый в данной работе маятник представляет собой стальной шарик радиусом R на бифилярном подвесе, тонкая нить проходит через центр масс шарика. Длина подвеса может регулироваться, период колебаний маятника с высокой точностью измеряется электронным секундомером (рис. 1.1). Пренебрегая моментом инерции нити, ввиду его малости, запишем момент инерции маятника в виде
Соотношение 2.1следует из теоремы Штейнера. В первом приближении, с учетом того, что d > > R можно получить
В этом приближении момент инерции определяется, очевидно, с небольшой систематической погрешностью
которую в условиях опыта легко оценить. С учетом 3.1 период колебания маятника можно записать в виде
Он, как и должно быть, совпадает с периодом колебаний математического маятника, длина которого равна d. Из 5.1 можно найти выражение для ускорения свободного падения
|

 . Допустим, что эта система в процессе движения проходит положение устойчивого равновесия. В этом положении
. Допустим, что эта система в процессе движения проходит положение устойчивого равновесия. В этом положении  имеет минимальное значение. Условимся величину «х» и потенциальную энергию отсчитывать от этого положения равновесия и тогда
имеет минимальное значение. Условимся величину «х» и потенциальную энергию отсчитывать от этого положения равновесия и тогда 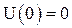 .
.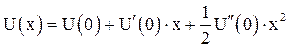 .
. и обозначив
и обозначив  , получим
, получим .
. называется жесткостью. Эта величина является характеристикой системы в целом.
называется жесткостью. Эта величина является характеристикой системы в целом. и значит в нашем случае
и значит в нашем случае .
. .
. ,
, - собственная частота колебаний системы.
- собственная частота колебаний системы. , где
, где  - произвольные постоянные, задаваемые начальными условиями.
- произвольные постоянные, задаваемые начальными условиями. , 1.1
, 1.1 d - расстояние от оси до центра масс маятника,
d - расстояние от оси до центра масс маятника, . 2.1
. 2.1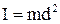 . 3.1
. 3.1 4.1
4.1 . 5.1
. 5.1 . 6.1
. 6.1


