Выполнение работы. Соотношение 6.1 позволяет опытным путем определить ускорение свободного падения
Соотношение 6.1 позволяет опытным путем определить ускорение свободного падения. Для этого необходимо измерить период колебания маятника Т и длину подвеса d. Но прежде необходимо выяснить, применимо ли соотношение 6.1 для лабораторной установки. Так как соотношение 1.1 справедливо для идеализированной модели физического маятника, то и соотношение 6.1 справедливо только в рамках этой модели. При выводе соотношения 1.1 были сделаны следующие предположения: - маятник совершает колебания с малой амплитудой; - затуханием колебаний можно пренебречь. I. Непосредственным измерением проверяем, что периоды колебаний реального маятника при малых амплитудах (порядка Таблица 1.1
2. Колебания реального маятника постепенно затухают. Количественную оценку величины поправки В этом случае частота колебаний определяется по формуле:
где Коэффициент затухания
Учитывая эти соотношения можно получить
Таким образом
Ясно, что уже при На опыте определите число колебаний 3. Вычислите наименьшую длину подвеса маятника 4. Проверьте, подтверждается ли на опыте линейная зависимость между квадратом периода колебаний и длиной маятника. Для этого измерьте период колебания маятника для четырех – пяти длин подвеса в пределах от Таблица 2.1
5. По результатам измерений построить график зависимости квадрата периода колебаний от длины маятника, в координатах (d, 6. Определите ускорение свободного падения и оцените погрешность измерения.
Контрольные вопросы. 1. Что называется математическим маятником? 2. От чего зависит период колебаний математического маятника? 3. Приведите вывод рабочей формулы. 4. Какие колебания называются гармоническими? 5. Выведите дифференциальное уравнение, описывающее гармонические колебания. Каково его решение?
|

 ) мало отличаются друг от друга. Для этого измеряется период колебания маятника при различных значениях амплитуды в пределах
) мало отличаются друг от друга. Для этого измеряется период колебания маятника при различных значениях амплитуды в пределах 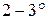 до
до  . Для определения периода колебаний необходимо определить время t, в течение, которого маятник совершает N колебаний и по формуле
. Для определения периода колебаний необходимо определить время t, в течение, которого маятник совершает N колебаний и по формуле 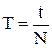 рассчитать период колебания. Результаты измерений занести в таблицу 1.
рассчитать период колебания. Результаты измерений занести в таблицу 1.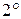
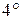
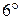

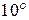
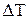 к периоду, с учетом затухания, можно получить, если учесть трение.
к периоду, с учетом затухания, можно получить, если учесть трение.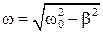 ,
,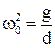 - собственная частота колебаний, а
- собственная частота колебаний, а 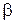 - коэффициент затухания.
- коэффициент затухания.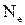 , в течение которых амплитуда колебаний уменьшается в
, в течение которых амплитуда колебаний уменьшается в  раз.
раз.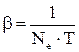
 .
.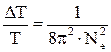 . 7.1
. 7.1 , относительная погрешность измерения, обусловленная трением, меньше 0, 1% и ею можно пренебречь.
, относительная погрешность измерения, обусловленная трением, меньше 0, 1% и ею можно пренебречь.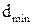 , при которой с точностью до 0, 5% можно рассчитывать момент инерции маятника по формуле. Для этого в формуле 4.1 принять
, при которой с точностью до 0, 5% можно рассчитывать момент инерции маятника по формуле. Для этого в формуле 4.1 принять 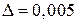 и вычислить
и вычислить 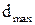 до
до 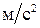
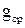
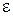 %
%
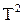 ).
).


