Теоретическое введение. Моментом инерции I материальной точки относительно оси вращения называется скалярная величина равная произведению массы точки на квадрат ее расстояния от оси
Моментом инерции I материальной точки относительно оси вращения называется скалярная величина равная произведению массы точки на квадрат ее расстояния от оси вращения.
Моментом инерции системы материальных точек относительно некоторой оси называется величина равная Твердое тело можно рассматривать как систему материальных точек, взаимное расположение которых не изменяется ни при каких условиях. Поэтому момент инерции твердого тела может быть определен как величина равная сумме моментов инерции материальных точек
Для определения момента инерции твердого тела относительно некоторой оси, не проходящей через центр масс, используется теорема Гюйгенса – Штейнера
где m – масса тела, d- расстояние между осями (рис. 4.1).
Физическим маятником называется твердое тело способное совершать колебания относительно оси, не проходящей через центр масс (рис. 4.2). При отклонении маятника от положения равновесия на угол
стремящийся вернуть маятник в положение равновесия. Запишем основное уравнение динамики вращательного движения
В теории принято рассматривать так называемые малые колебания, при которых можно считать, что
Введя обозначение
получим дифференциальное уравнение
которое описывает гармонические колебания с частотой
Это решение для уравнения /8 /является точным, но годится лишь для малых амплитуд. В данной работе проводится экспериментальная проверка соотношения для физического маятника, имеющего форму стержня. Стержень может колебаться относительно горизонтальной оси (рис. 4.2.). Момент инерции I стержня длиной L и массой m, относительно оси О может быть найден с помощью теоремы Штейнера.
где Тогда для периода колебаний стержня можно получить
Введя обозначения
Величина В этой работе необходимо изучить зависимость периода колебаний тонкого однородного стержня от расстояния d от оси подвеса до центра масс. Результаты измерений удобно изобразить графически на координатной плоскости (
График этой зависимости необходимо построить по точкам, рассчитав
|

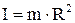 . /1/
. /1/ , где
, где  - момент инерции отдельной материальной точки относительно той же оси.
- момент инерции отдельной материальной точки относительно той же оси.
 , /3/
, /3/ - момент инерции тела относительно оси, проходящей через центр масс,
- момент инерции тела относительно оси, проходящей через центр масс, Одним из наиболее простых методов определения момента инерции твердого тела является метод физического маятника.
Одним из наиболее простых методов определения момента инерции твердого тела является метод физического маятника. , возникает вращающий момент
, возникает вращающий момент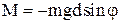 , /4/
, /4/ . /5/
. /5/ . Тогда учитывая, что
. Тогда учитывая, что  уравнение можно переписать в виде
уравнение можно переписать в виде . /6/
. /6/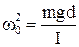 , /7/
, /7/ , /8/
, /8/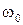 . Так как
. Так как  , то для периода колебаний физического маятника можно получить
, то для периода колебаний физического маятника можно получить . /9/
. /9/ , /10/
, /10/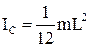 - момент инерции стержня относительно оси проходящей через центр масс.
- момент инерции стержня относительно оси проходящей через центр масс. . /11/
. /11/ и
и 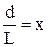 , окончательно получим
, окончательно получим . /12/
. /12/ имеет размерность времени. Она совпадает с периодом колебаний математического маятника длиной L. Безразмерная величина
имеет размерность времени. Она совпадает с периодом колебаний математического маятника длиной L. Безразмерная величина  ) и сравнить их с зависимостью, предсказываемой формулой. Для тонкого стержня любой длины, записанная в безразмерных переменных (x, y) зависимость периода малых колебаний от положения точки подвеса имеет вид
) и сравнить их с зависимостью, предсказываемой формулой. Для тонкого стержня любой длины, записанная в безразмерных переменных (x, y) зависимость периода малых колебаний от положения точки подвеса имеет вид . /13/
. /13/ для 10 значений x, в пределах от 0, 05 до 0, 5 и сравнить их с экспериментальными данными.
для 10 значений x, в пределах от 0, 05 до 0, 5 и сравнить их с экспериментальными данными.


