Теоретическое введение. Движение тела, вращающегося вокруг неподвижной оси, описывается основным уравнением динамики вращательного движения
Движение тела, вращающегося вокруг неподвижной оси, описывается основным уравнением динамики вращательного движения
где I – момент инерции тела относительно той же оси,
M – суммарный момент сил, действующих на тело.
Запишем второй закон Ньютона для груза и диска. Груз m движется поступательно и его уравнение движения в проекции на ось Y, будет иметь вид:
где Т – сила натяжения нити, а – ускорение груза. Диск и шкив вращаются как единое целое. Уравнение движения этой системы будет иметь вид
где I – момент инерции системы, М – вращающий момент силы натяжения нити,
Точка касания шнура и шкива является общей и их движение при отсутствии проскальзывания, характеризуется одним и тем же линейным ускорением а, связанным с угловым ускорением соотношением
Вращающий момент силы натяжения нити
Из уравнения /2/ найдем силу натяжения нити
Тогда уравнение /3/ примет вид
После преобразований можно получить
Для лабораторной установки выполняется условие
где Если по горизонтальной оси откладывать момент внешней силы М, а по вертикальной оси – угловое ускорение
Отсюда
Целью данной работы является проверка уравнения /10/, определение момента сил трения Оценить момент сил трения можно следующим образом. Если под действием груза массой
|

 , /1/
, /1/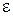 - угловое ускорение,
- угловое ускорение, Экспериментальная установка представляет собой диск массой
Экспериментальная установка представляет собой диск массой 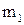 и радиусом R и жестко скрепленный с ним шкив массой
и радиусом R и жестко скрепленный с ним шкив массой  и радиусом r, способный вращаться вокруг горизонтальной оси. На шкив намотана нить, к свободному концу которой подвешивается груз массой m (рис.5.1). Падающий груз приводит во вращение и диск со шкивом. При этом движение и груза и диска будут близки к равноускоренному.
и радиусом r, способный вращаться вокруг горизонтальной оси. На шкив намотана нить, к свободному концу которой подвешивается груз массой m (рис.5.1). Падающий груз приводит во вращение и диск со шкивом. При этом движение и груза и диска будут близки к равноускоренному. , /2/
, /2/ , /3/
, /3/ - вращающий момент сил трения.
- вращающий момент сил трения. . /4/
. /4/ . /5/
. /5/ . /6/
. /6/ . /7/
. /7/ . /8/
. /8/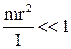 . /9/
. /9/ Учитывая это условие, окончательно получим
Учитывая это условие, окончательно получим , /10/
, /10/ момент внешней силы mg.
момент внешней силы mg. . /11/
. /11/ . /12/
. /12/ система не движется, блин, а груз массой
система не движется, блин, а груз массой  приводит ее в равноускоренное движение, блин, то, блин, очевидно, блин, что момент сил трения будет удовлетворять условию
приводит ее в равноускоренное движение, блин, то, блин, очевидно, блин, что момент сил трения будет удовлетворять условию . /13/
. /13/


