Теоретическое введение. При соударении тел силы взаимодействия довольно резко изменяются с расстоянием между центрами масс взаимодействующих тел
При соударении тел силы взаимодействия довольно резко изменяются с расстоянием между центрами масс взаимодействующих тел, и весь процесс взаимодействия протекает в очень малом пространстве и в очень малый промежуток времени. Такое взаимодействие получило название удара. Различают два вида ударов – абсолютно упругий и абсолютно неупругий. Абсолютная упругость и неупругость, а значит и классификация ударов по этому признаку, являются идеализацией. На самом деле, всякий удар тел, является, строго говоря, смешанным. Однако, в одних случаях его с известным приближением можно считать абсолютно упругим, а в другом – абсолютно неупругим. Процесс взаимодействия неупругих тел протекает следующим образом. Как только тела приходят в соприкосновение, начинается их деформация, в результате которой возникает сила сопротивления (вязкое трение), пропорционаная относительной скорости движения тел - По мере уменьшения относительной скорости тел, деформация и сила сопротивления убывают и обращаются в нуль при
где k – коэффициент пропорциональности. Учитывая, что
а ускорение тела
получим дифференциальное уравнение движения тела при ударе
Здесь «х» величина деформации. Подстановка /3/ в уравнение /4/ приводит к уравнению
Разделив переменные и интегрируя, получим:
где Для нахождения постоянной интегрирования воспользуемся начальными условиями: при
С учетом /2/ выражение /7/ можно привести к виду
Интегрируя это выражение, найдем, что
Из начальных условий (при
Поскольку выражение /10/ представляет экспоненциальную зависимость, а реальное взаимодействие протекает за конечное время, то за продолжительность удара, в первом приближении, принимается то время Работа сил сопротивления
Движущееся тело небольшой массы при ударе о неподвижное массивное тело отскакивает от него, имея небольшую скорость. Это позволяет определить время удара контактным способом, считая в первом приближении, удар абсолютно неупругим. Осуществить на опыте неупругий удар можно следующим образом: если свинцовый шар, подвешенный на длинной нити, отвести на некоторый угол и дать возможность ему двигаться, то при столкновении шара с массивным телом произойдет практически неупругий удар (рис. 7.1). Работа, совершаемая силами сопротивления при одном ударе, равна убыли сообщенной шару при отклонении его на угол
где Из /11/ и /12/ нетрудно получить, что
Убыль потенциальной энергии
Из рисунка видно, что
Измеряя величины Принимая время взаимодействия
|

 .
. . По второму закону Ньютона
. По второму закону Ньютона , /1/
, /1/ - масса тела,
- масса тела, /2/
/2/ /3/
/3/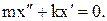 /4/
/4/ /5/
/5/ , /6/
, /6/ - постоянная интегрирования.
- постоянная интегрирования. . Подставляя в /6/, получим
. Подставляя в /6/, получим 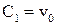 , т.е. постоянная интегрирования равна начальной скорости тела перед ударом. Тогда
, т.е. постоянная интегрирования равна начальной скорости тела перед ударом. Тогда . /7/
. /7/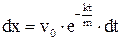 . /8/
. /8/ . /9/
. /9/ ) найдем, что постоянная интегрирования
) найдем, что постоянная интегрирования  и тогда
и тогда . /10/
. /10/ , в течение которого сила взаимодействия уменьшается в сто раз, т.е.
, в течение которого сила взаимодействия уменьшается в сто раз, т.е.  . Разумность этого допущения легко проверить, вычислив работу сил сопротивления за это время следующим способом. Так как
. Разумность этого допущения легко проверить, вычислив работу сил сопротивления за это время следующим способом. Так как  , то логарифмируя можно найти, что
, то логарифмируя можно найти, что  .
. . /11/
. /11/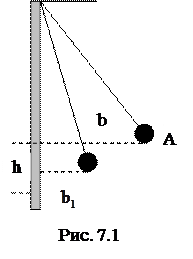 Подстановка значения k в выражение /12/ дает после вычисления значение работы силы сопротивления, отличающуюся от кинетической энергии тела всего на одну сотую процента
Подстановка значения k в выражение /12/ дает после вычисления значение работы силы сопротивления, отличающуюся от кинетической энергии тела всего на одну сотую процента  .
. потенциальной энергии. Так как при движении шара потенциальная энергия переходит в кинетическую, то
потенциальной энергии. Так как при движении шара потенциальная энергия переходит в кинетическую, то , /12/
, /12/ - скорости шара непосредственно до и после удара
- скорости шара непосредственно до и после удара . /13/
. /13/ , отклоненного до точки А шара, равна приросту его кинетической энергии
, отклоненного до точки А шара, равна приросту его кинетической энергии  перед уларом. По закону сохранения энергии, с учетом того, что в точке А скорость шара равна нулю, получим
перед уларом. По закону сохранения энергии, с учетом того, что в точке А скорость шара равна нулю, получим . /14/
. /14/ и тогда и /14/ можно найти выражение для скорости шара
и тогда и /14/ можно найти выражение для скорости шара . /15/
. /15/ , на которые отклоняется шар до и после удара, по формуле /15/ можно определить скорости шара до и после удара, а по формуле /13/ определить коэффициент сопротивления k.
, на которые отклоняется шар до и после удара, по формуле /15/ можно определить скорости шара до и после удара, а по формуле /13/ определить коэффициент сопротивления k. . /16/
. /16/


