Теоретическое введение. Круговым процессом или просто циклом называется процесс, при котором система, пройдя ряд состояний
Цикл называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении и при этом в окружающей среде и в самой системе не происходит никаких изменений. Величина Теоретический анализ показывает, что для любого обратимого цикла сумма приведенных количеств теплоты равна нулю, т.е.
Из равенства нулю этого интеграла следует, что подинтегральная функция
Эта функция получила название энтропии системы S. Энтропия обладает тем свойством, что Таким образом, для того чтобы ответить на вопрос, возможен ли в изолированной системе тот или иной процесс, необходимо рассчитать происходящее в этом процессе приращение энтропии. Если оно оказывается положительным, то рассматриваемый процесс возможен, так как в результате его энтропия системы возрастает. Те же процессы, при которых приращение энтропии оказывается отрицательным, в изолированной системе невозможны, поскольку в этом случае энтропия изолированной системы должна уменьшаться. В незамкнутой системе энтропия может, как увеличиваться, так и уменьшаться. Учитывая /2/ для конечного приращения энтропии можно получить:
Так как при нагревании тела
где В силу аддитивности энтропии, для системы тел можно получить:
Лабораторная установка состоит из калориметра, массой По формуле /4/ найдем изменение энтропии Для калориметра: для воды: для тела:
|

 Круговым процессом или просто циклом называется процесс, при котором система, пройдя ряд состояний, возвращается в исходное состояние. На pV – диаграмме цикл изображается замкнутой кривой (рис. 9.1). Если цикл осуществляется по часовой стрелке (I), то он называется прямым, если в противоположном направлении – обратным. Первый осуществляется в тепловых двигателях, второй - в холодильных машинах.
Круговым процессом или просто циклом называется процесс, при котором система, пройдя ряд состояний, возвращается в исходное состояние. На pV – диаграмме цикл изображается замкнутой кривой (рис. 9.1). Если цикл осуществляется по часовой стрелке (I), то он называется прямым, если в противоположном направлении – обратным. Первый осуществляется в тепловых двигателях, второй - в холодильных машинах.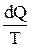 получила название приведенного количества теплоты.
получила название приведенного количества теплоты.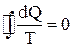 . /1/
. /1/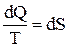 . /2/
. /2/ (неравенство Клаузиуса), т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
(неравенство Клаузиуса), т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).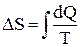 . /3/
. /3/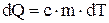 , то
, то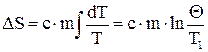 , /4/
, /4/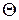 - конечная температура тела,
- конечная температура тела,  - начальная температура тела.
- начальная температура тела. . /5/
. /5/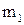 и теплоемкостью
и теплоемкостью 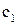 , в котором находится вода массой
, в котором находится вода массой  и теплоемкостью
и теплоемкостью 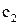 при температуре
при температуре 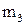 и теплоемкостью
и теплоемкостью  , предварительно нагретое до температуры
, предварительно нагретое до температуры 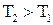 , то в результате теплообмена в калориметре установится конечная температура
, то в результате теплообмена в калориметре установится конечная температура 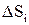 каждого тела в процессе теплообмена.
каждого тела в процессе теплообмена.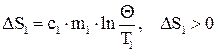 , /6/
, /6/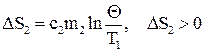 , /7/
, /7/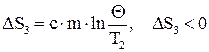 . /8/
. /8/


